题目内容
如图甲所示,两平行金属板A、B的板长L=0.2m,板间距d=0.2m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应.在金属板右侧有一方向垂直于纸面向里的匀强磁场,其左右宽度D=0.4m,上下范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B=1×10-2 T.现从t=0开始,从两极板左侧的中点O处以每秒钟1000个的数量均匀连续地释放出某种正电荷粒子,这些粒子均以v=2×105 m/s的速度沿两板间的中线OO′连续进入电场,已知带电粒子的比荷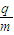 =1×108C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:
=1×108C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:(1)t=0时刻进入的粒子,经边界MN射入磁场和射出磁场时两点间的距离;
(2)在0~1s内有多少个带电粒子能进入磁场;
(3)何时由O点进入的带电粒子在磁场中运动的时间最长?
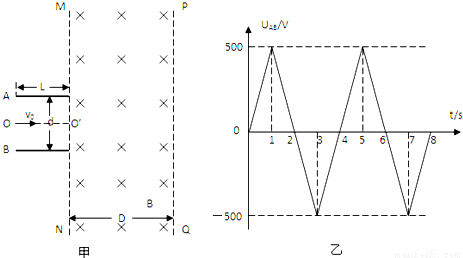
【答案】分析:(1)t=0时刻,电压为0,故粒子在电场中不会发生偏转,由洛仑兹力充当向心力公式可得出粒子的偏转半径;由几何关系可得出入射点与出射点间的距离;
(2)随着电压的增大,粒子的偏转位移也增大;则能穿出电场的临界条件是粒子恰好打在板的最右端;由类平抛运动的规律可求得临界电压;由图可求得能进入磁场的粒子个数;
(3)要使粒子运动时间最长,则粒子在磁场中转过的圆心角应最大;由几何关系可知,当粒子的轨迹与PQ相切时,其运动时间最长.
解答:解:(1)t=0时刻,电压为0,粒子匀速通过两板进入磁场,
qvB=m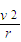
r=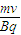 =0.2m
=0.2m
r<D,则粒子在MN边界射出磁场.
入射点和出射点的距离为s=2r=0.4m
(2)粒子在两板间做类平抛运动,刚好打到板最右端时,
L=vt1
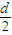 =
= at12
at12
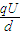 =ma
=ma
U=400V
则0~1s内能够进入磁场的粒子个数为n=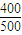 ×1000=800
×1000=800
(3)假设两板加电压为U时,粒子向下偏转并进入磁场,刚好与磁场PQ边界相切,
在磁场中,qvB=m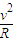
由几何关系得,R+Rsinθ=D
在电场中,v=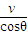
联立解得:θ=37
vy=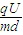 t1=vtanθ
t1=vtanθ
U=300V
U<U=400V,则当两板电压U=300V,且粒子向下偏转时,粒子在磁场中运动的时间最长,对应入射的时刻为
t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2…)
答:(1)入射点和出射点的距离为0.4m;
(2)0~1s内能够进入磁场的粒子个数为800个;
(3)粒子在磁场中运动的时间最长,对应入射的时刻为t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2…)
点评:本题应注意题意中给出的条件,在粒子穿出电场的时间极短,电压看作不变;同时要注意带电粒子在磁场中的偏转类题目一定要找清几何关系.
(2)随着电压的增大,粒子的偏转位移也增大;则能穿出电场的临界条件是粒子恰好打在板的最右端;由类平抛运动的规律可求得临界电压;由图可求得能进入磁场的粒子个数;
(3)要使粒子运动时间最长,则粒子在磁场中转过的圆心角应最大;由几何关系可知,当粒子的轨迹与PQ相切时,其运动时间最长.
解答:解:(1)t=0时刻,电压为0,粒子匀速通过两板进入磁场,
qvB=m
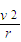
r=
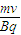 =0.2m
=0.2m r<D,则粒子在MN边界射出磁场.
入射点和出射点的距离为s=2r=0.4m
(2)粒子在两板间做类平抛运动,刚好打到板最右端时,
L=vt1
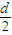 =
= at12
at12 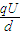 =ma
=ma U=400V
则0~1s内能够进入磁场的粒子个数为n=
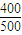 ×1000=800
×1000=800(3)假设两板加电压为U时,粒子向下偏转并进入磁场,刚好与磁场PQ边界相切,
在磁场中,qvB=m
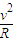
由几何关系得,R+Rsinθ=D
在电场中,v=
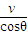
联立解得:θ=37
vy=
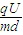 t1=vtanθ
t1=vtanθU=300V
U<U=400V,则当两板电压U=300V,且粒子向下偏转时,粒子在磁场中运动的时间最长,对应入射的时刻为
t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2…)
答:(1)入射点和出射点的距离为0.4m;
(2)0~1s内能够进入磁场的粒子个数为800个;
(3)粒子在磁场中运动的时间最长,对应入射的时刻为t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2…)
点评:本题应注意题意中给出的条件,在粒子穿出电场的时间极短,电压看作不变;同时要注意带电粒子在磁场中的偏转类题目一定要找清几何关系.

练习册系列答案
相关题目
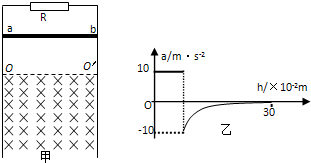 (2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
(2011?徐州一模)如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:

 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: =1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45=
=1x108C/kg、初速度v0=2x 105m/s的带正电粒子.忽略粒子重力、粒子间相互作用以及粒子在极板间飞行时极 板间的电压变化.sin30=0.5,sin37=0.6,sin45= .
.