题目内容
以初速度为y0,水平方向位移为S的某质点平抛运动轨迹制成一光滑轨道.如图所示,一质量为m的小环套在该轨道上,由静止开始从其顶端滑下,当小环到达轨道底端时(已知重力加速度为g),求:
①小环的速率.
②小环水平方向的速度大小.
①小环的速率.
②小环水平方向的速度大小.
分析:物体在轨道上滑下,受重力和支持力,但只有重力做功,机械能守恒,由机械能守恒定律求出物体到达轨道底部时的速率.再把这时的速度向水平方向分解求水平方向的速度大小,不过必须先由原来的平抛运动求出轨道底部的速度偏离水平方向的角度,然后通过解三角函数关系求水平方向的速度大小.
解答:解:(1)由平抛运动规律知:
水平方向做匀速运动:s=υ0t
竖直方向做自由落体运动:h=
gt2
解得轨道的高度h=
小环从轨道顶端由静止滑到底端时,根据机械能守恒定律得:mgh=
mυ2
解得v=
(2)设小环在轨道底端时的速度方向与水平的夹角为θ,
则tanθ=
=
=
物块落到轨道底端时水平分速度υx=υcosθ
由以上两式得υx=
答:①小环的速率是v=
.
②小环水平方向的速度大小
.
水平方向做匀速运动:s=υ0t
竖直方向做自由落体运动:h=
| 1 |
| 2 |
解得轨道的高度h=
| gs2 |
| 2υ02 |
小环从轨道顶端由静止滑到底端时,根据机械能守恒定律得:mgh=
| 1 |
| 2 |
解得v=
| gs |
| v0 |
(2)设小环在轨道底端时的速度方向与水平的夹角为θ,
则tanθ=
| vy |
| v0 |
| ||
| v0 |
| gs |
| v02 |
物块落到轨道底端时水平分速度υx=υcosθ
由以上两式得υx=
| v0 | ||||||
|
答:①小环的速率是v=
| gs |
| v0 |
②小环水平方向的速度大小
| v0 | ||||||
|
点评:本题速度的分解是按轨道的切线分解,而轨道的切线方向即为平抛的速度方向,平抛的速度方向与水平方方向夹角θ的正切等于位移方向与水平方向夹角α的正切的2倍,学生容易错在直接用tanα计算cosθ,把两个角混为一谈.因此要注重应用数学解物理题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图所示,为“研究平抛物体的运动”的实验装置.
如图所示,为“研究平抛物体的运动”的实验装置.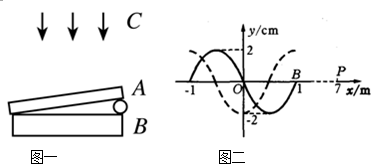
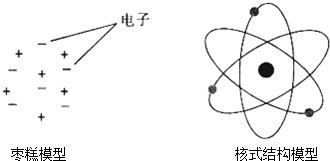
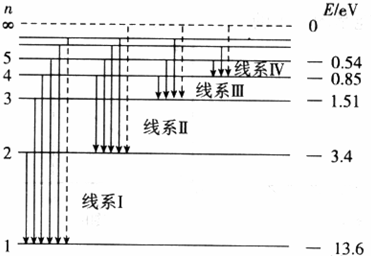

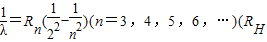 为常数)
为常数)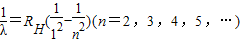 (RH为常数)
(RH为常数)