题目内容
如图5所示，台秤上有一装水容器，底部用一质量不计的细线系住一个空心小球，体积为1.2×10-3m3，质量为1kg，这时台秤的读数为40N，剪断细线后，在小球上升的过程中，台秤的读数是多少？（ρ=1×103kg/m3）
见解析
【试题分析】
剪断细线后，小球加速上升，对小球由牛顿第二定律得ΣF=ρVg-mg=ma①
小球上升时，小球上方的水也以相同大小的加速度a加速向下流动以填补小球原来占据的空间，那么其水的质量为m′=ρV=1.2kg ②
对容器整体，同理可得台秤对容器的支持力
F=40+ma+m′a ③
代入已知量解①②③得F=39.6N，即台秤的读数是39.6N.
练习册系列答案
相关题目
物理兴趣小组活动中，小红提出如下问题：“电梯上升过程中有什么运动规律？”小明同学决定通过实验来探究这一问题．
图5
物理兴趣小组活动中，小红提出如下问题：“电梯上升过程中有什么运动规律？”小明同学决定通过实验来探究这一问题．
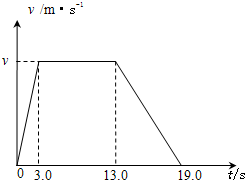
小明选择了台秤、钩码和停表等仪器进行实验，经过多次仔细的观察和测量，他探究出了电梯上升过程中速度随时间的变化规律（v-t图象），如图所示．
下面是小明的某次实验情况：他将台秤水平放置在电梯内，并把一质量m=0.5kg的钩码放在台秤的托盘上，电梯从第一层开始启动经过不间断地运行，最后停在最高层．在整个过程中，他记录下了台秤在不同时间段内的示数，记录的数据如下表所示，但由于疏忽，小明没有记录下13.0～19.0s 时间段内台秤的示数．请通过分析或计算解答下列问题：（设在每个时间段内台秤的示数都是稳定的，重力加速度g取10m/s2．）
（1）请你根据v-t图象及表格中的数据，判断在0～3.0s、3.0～13.0s、13.0～19.0s时间段内，电梯内的钩码所处的超、失重状态，并将判断的结果填入表格内相应的位置．
（2）在0～3.0s内，钩码的加速度大小是多少？
（3）v-t图象中电梯做匀速运动时的速度v是多少？
（4）电梯在13.0～19.0s 时间段内台秤的示数应该是多少？
| 时间（s） | 台秤示数（N） | 钩码超、失重判断 |
| 电梯启动前 | 5.0 | |
| 0～3.0 | 5.8 | |
| 3.0～13.0 | 5.0 | |
| 13.0～19.0 | ？ | |
| 19.0以后 | 5.0 |