Question

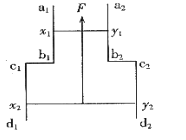
【题目】如图所示，左侧正方形区域ABCD有竖直方向的匀强电场和垂直纸面方向的磁场，右侧正方形区域CEFG有电场，一质量为m，带电量为+q的小球，从距A点正上方高为L的O点静止释放进入左侧正方形区域后做匀速圆周运动，从C点水平进入右侧正方形区域CEFG．已知正方形区域的边长均为L，重力加速度为g，求：

（1）左侧正方形区域的电场强度E1和磁场的磁感应强度B；

（2）若在右侧正方形区域内加竖直向下的匀强电场，能使小球恰好从F点飞出，求该电场场强E2的大小；

（3）若在右侧正方形区域内加水平向左的匀强电场，场强大小为（k为正整数），试求小球飞出该区域的位置到G点的距离．

Answer 1

【答案】（1），方向竖直向上；，方向垂直纸面向外（2）（3）①L②

【解析】

（1）

小球做匀速圆周运动 解得：，方向竖直向上

由几何关系，又

解得：，方向垂直纸面向外

（2）在CEFG区域，小球做类平抛运动，

水平方向：，解得

竖直方向：，解得

又，

解得

（3）水平方向：，解得

竖直方向小球做自由落体运动.

当水平方向减速至零时，用时

由，解得，

①当k=1时，x=L，小球水平方向恰好到达FG边，此时竖直位移=L，小球恰好从F点飞出，此时距G点L。

②当k=2，3，4……时，x<L，竖直位移=≤L，小球从CG边飞出，此时距G点