题目内容
如图18所示,一质量为M 、倾角为θ的光滑斜面,放置在光滑的水平面上,另一个质量为m的滑块从斜面顶端释放,试求斜面的加速度。

解说:本题涉及两个物体,它们的加速度关系复杂,但在垂直斜面方向上,大小是相等的。对两者列隔离方程时,务必在这个方向上进行突破。
(学生活动)定型判断斜面的运动情况、滑块的运动情况。
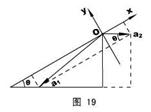
位移矢量示意图如图19所示。根据运动学规律,加速度矢量a1和a2也具有这样的关系。
(学生活动)这两个加速度矢量有什么关系?
沿斜面方向、垂直斜面方向建x 、y坐标,可得:a1y = a2y①
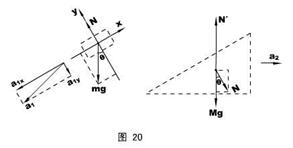
且:a1y = a2sinθ② 隔离滑块和斜面,受力图如图20所示。
对滑块,列y方向隔离方程,有:mgcosθ- N = ma1y③
对斜面,仍沿合加速度a2方向列方程,有:Nsinθ= Ma2④
解①②③④式即可得a2 。
答案:a2 = ![]() 。
。
(学生活动)思考:如何求a1的值?
解:a1y已可以通过解上面的方程组求出;a1x只要看滑块的受力图,列x方向的隔离方程即可,显然有mgsinθ= ma1x ,得a1x = gsinθ 。最后据a1 = ![]() 求a1 。
求a1 。
答:a1 = ![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1)图1为氢原子能级的示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干不同频率的光.关于这些光下列说法正确的是
(1)图1为氢原子能级的示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干不同频率的光.关于这些光下列说法正确的是

















 g
g
 。
。





