题目内容
 屋檐间隔一定时间滴出一滴水,当第5滴正欲滴下时,第1滴刚好到达地面,而第3滴与第2滴正分别位于高1m的窗户的上、下沿,如图2-5所示.取g=10m/s2,试求:
屋檐间隔一定时间滴出一滴水,当第5滴正欲滴下时,第1滴刚好到达地面,而第3滴与第2滴正分别位于高1m的窗户的上、下沿,如图2-5所示.取g=10m/s2,试求:
(1)此屋檐离地面的高度;
(2)相临两滴水的时间间隔.
解:(1)根据比例关系,从上到下相邻水滴间距离之比为1:3:5:7,而2、3两滴间距离为1米,所以总高度H= ×1=3.2m
×1=3.2m
(2)根据H= gt2,代入数据得,t=
gt2,代入数据得,t=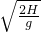 =
= s=0.8s
s=0.8s
滴水时间间隔△t= =0.2s
=0.2s
答:(1)此屋檐离地面的高度3.2m;
(2)相临两滴水的时间间隔0.2s.
分析:(1)初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.已知第3滴与第2滴水的间隔距离,根据比例关系求出总高度.
(2)由H= gt2,得出水从屋檐到地面的时间,从而得出相等的时间间隔.
gt2,得出水从屋檐到地面的时间,从而得出相等的时间间隔.
点评:解决本题的关键掌握初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.以及掌握自由落体运动的位移时间公式H= gt2.
gt2.
 ×1=3.2m
×1=3.2m(2)根据H=
 gt2,代入数据得,t=
gt2,代入数据得,t=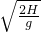 =
= s=0.8s
s=0.8s滴水时间间隔△t=
 =0.2s
=0.2s答:(1)此屋檐离地面的高度3.2m;
(2)相临两滴水的时间间隔0.2s.
分析:(1)初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.已知第3滴与第2滴水的间隔距离,根据比例关系求出总高度.
(2)由H=
 gt2,得出水从屋檐到地面的时间,从而得出相等的时间间隔.
gt2,得出水从屋檐到地面的时间,从而得出相等的时间间隔.点评:解决本题的关键掌握初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.以及掌握自由落体运动的位移时间公式H=
 gt2.
gt2. 
练习册系列答案
相关题目
 屋檐间隔一定时间滴出一滴水,当第5滴正欲滴下时,第1滴刚好到达地面,而第3滴与第2滴正分别位于高1m的窗户的上、下沿,如图2-5所示.取g=10m/s2,试求:
屋檐间隔一定时间滴出一滴水,当第5滴正欲滴下时,第1滴刚好到达地面,而第3滴与第2滴正分别位于高1m的窗户的上、下沿,如图2-5所示.取g=10m/s2,试求:

