题目内容
如图所示,左侧匀强电场的区域宽度为L,电场强度为E,右侧匀强磁场的左右宽度为d,磁场的上下区域很长,一质量为m、带电量为q的粒子,从电场的左边界A点静止释放,经电场加速后垂直进入磁场,出磁场时与入射方向的偏角为θ.(不计粒子重力)求:(1)粒子离开电场时的速度;
(2)匀强磁场的磁感应强度;
(3)粒子在磁场中的运动时间.

【答案】分析:(1)设粒子经电场加速后的速度为v,根据动能定理即可求解;
(2)根据洛仑兹力提供向心力及几何关系即可求解;
(3)粒子在磁场中做圆周运动,根据圆周运动的周期公式即可解题.
解答: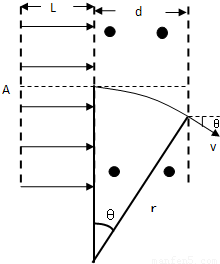 解:(1)在电场中电场力做功等于粒子的动能:
解:(1)在电场中电场力做功等于粒子的动能:
得
(2)在磁场中洛伦兹力提供向心力: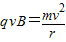
有几何关系 d=rsinθ
可得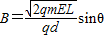
(3)由周期公式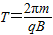
及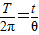
可得
答:(1)粒子离开电场时的速度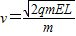 ;
;
(2)匀强磁场的磁感应强度 ;
;
(3)粒子在磁场中的运动时间 .
.
点评:点评:本题主要考查了带电粒子在组合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握圆周运动及平抛运动的基本公式,难度适中.
(2)根据洛仑兹力提供向心力及几何关系即可求解;
(3)粒子在磁场中做圆周运动,根据圆周运动的周期公式即可解题.
解答:
 解:(1)在电场中电场力做功等于粒子的动能:
解:(1)在电场中电场力做功等于粒子的动能:
得

(2)在磁场中洛伦兹力提供向心力:
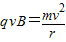
有几何关系 d=rsinθ
可得
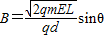
(3)由周期公式
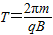
及
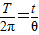
可得

答:(1)粒子离开电场时的速度
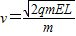 ;
;(2)匀强磁场的磁感应强度
 ;
;(3)粒子在磁场中的运动时间
 .
.点评:点评:本题主要考查了带电粒子在组合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握圆周运动及平抛运动的基本公式,难度适中.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图所示,左侧为二块长为L=10cm,间距d=
如图所示,左侧为二块长为L=10cm,间距d=


 cm的平行金属板,加U=
cm的平行金属板,加U= 的电压,上板电势高;现从左端沿中心轴线方向入射一个重力不计的带电微粒,微粒质量m=10-10kg,带电量q=+10-4C,初速度v0=105m/s;中间用虚线框表示的正三角形内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板平齐,BC边与金属板平行,AB边的中点P1恰好在下金属板的右端点;三角形区域的右侧也存在垂直纸面向里,范围足够大的匀强磁场B2,且B2=4B1;求;
的电压,上板电势高;现从左端沿中心轴线方向入射一个重力不计的带电微粒,微粒质量m=10-10kg,带电量q=+10-4C,初速度v0=105m/s;中间用虚线框表示的正三角形内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板平齐,BC边与金属板平行,AB边的中点P1恰好在下金属板的右端点;三角形区域的右侧也存在垂直纸面向里,范围足够大的匀强磁场B2,且B2=4B1;求;