题目内容
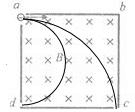
 如图所示,截面为正方形空腔abcd中有一匀强磁场,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的电子都被腔壁吸收,则由小孔c和小孔d射出的电子的速率之比为
如图所示,截面为正方形空腔abcd中有一匀强磁场,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的电子都被腔壁吸收,则由小孔c和小孔d射出的电子的速率之比为分析:带电粒子在磁场中做圆周运动,由几何知识可分别求得从c点和d点飞出的粒子的半径,则由向心力公式可求得各自的速率及比值;由转动的角度可知运动时间之比.
解答:解:设磁场边长为a,如图所示,粒子从c点离开,其半径为a;
由BqVc=m
可得:
Vc=
;
粒子从d点离开,其半径为
;
则Vd=
故
=
;
粒子的运行周期T=
;
从c点离开的粒子运行的时间tc=
从d点离开的粒子运行的时间td=
;
故
=
;
故答案为:2:1;1:2.

由BqVc=m
| ||
| a |
Vc=
| Bqa |
| m |
粒子从d点离开,其半径为
| a |
| 2 |
则Vd=
| Bqa |
| 2m |
故
| Vc |
| Vd |
| 2 |
| 1 |
粒子的运行周期T=
| 2πm |
| Bq |
从c点离开的粒子运行的时间tc=
| T |
| 4 |
从d点离开的粒子运行的时间td=
| T |
| 2 |
故
| tc |
| td |
| 1 |
| 2 |
故答案为:2:1;1:2.
点评:本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






 s时刻速度为0
s时刻速度为0 、
、 。
。



 /2或者
/2或者
