题目内容
 为了探究滑行者在某景点的山坡滑道直线AE滑行的时间,技术人员通过测量绘制出如图所示的示意图,AC是滑道的竖直高度,D点是AC竖直线上的一点,且有AD=DE=20m,滑道AE可视为光滑,滑行者从坡顶A点由静止开始沿滑道AE向下做直线滑动,g取l0m/s2,则滑行者在滑道AE上滑行的时间为( )
为了探究滑行者在某景点的山坡滑道直线AE滑行的时间,技术人员通过测量绘制出如图所示的示意图,AC是滑道的竖直高度,D点是AC竖直线上的一点,且有AD=DE=20m,滑道AE可视为光滑,滑行者从坡顶A点由静止开始沿滑道AE向下做直线滑动,g取l0m/s2,则滑行者在滑道AE上滑行的时间为( )分析:设斜面坡角为θ,从D向AE做垂线交于点F,由AD=DE=20m,得AF=20×sinθ,故AE=2AF=40sinθ;再根据牛顿第二定律求解出加速度,然后根据匀加速直线运动的位移时间关系公式列式求解即可.
解答:解:设斜面坡角为θ,则:AE=2AF=40sinθ…①
物体做匀加速直线运动,对物体受力分析,受重力和支持力,将重力沿着平行斜面和垂直斜面正交分解,根据牛顿第二定律,有:
mgsinθ=ma
解得:a=gsinθ…②
根据速度位移公式,有:
AE=
at2…③
由①②③式,解得:t=2
s.所以选项D正确.
故选:D.
物体做匀加速直线运动,对物体受力分析,受重力和支持力,将重力沿着平行斜面和垂直斜面正交分解,根据牛顿第二定律,有:
mgsinθ=ma
解得:a=gsinθ…②
根据速度位移公式,有:
AE=
| 1 |
| 2 |
由①②③式,解得:t=2
| 2 |
故选:D.
点评:本题关键是根据牛顿第二定律求解出加速度,然后根据位移时间关系公式列式求解,关键是有中间变量θ,要列式后约去.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (2011?江西模拟)如图甲是某景点的山坡滑道图片,为了探究滑行者在滑道直线部分AE滑行的时间.技术人员通过测量绘制出如图乙所示的示意图.AC是滑道的竖直高度,D点是AC竖直线上的一点,且有AD=DE=10m,滑道AE可视为光滑,滑行者从坡顶A点由静止开始沿滑道AE向下做直线滑动,g取10m/s2,则滑行者在滑道AE上滑行的时间为( )
(2011?江西模拟)如图甲是某景点的山坡滑道图片,为了探究滑行者在滑道直线部分AE滑行的时间.技术人员通过测量绘制出如图乙所示的示意图.AC是滑道的竖直高度,D点是AC竖直线上的一点,且有AD=DE=10m,滑道AE可视为光滑,滑行者从坡顶A点由静止开始沿滑道AE向下做直线滑动,g取10m/s2,则滑行者在滑道AE上滑行的时间为( )
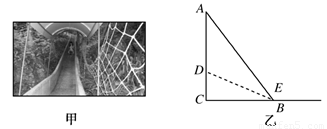
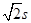 B.2 s
B.2 s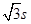 D.
D.