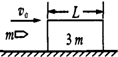
题目内容
如图所示,质量为3m的木板C放在水平面上,木板与地面的摩擦不计,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ,开始时木板静止,A、B两木块分别以水平向右的初速度2v。和v。在木板上滑动,若木板足够长,A、B始终未脱离木板,求A、B间的距离至少多大时,才能保证它们不相碰?
木块B先匀减速后与C一起匀加速,木块A一直匀减速,木板C做两段加速度不同的匀加速运动,最后A、B、C三者速度相同。对三物组成的系统,由动量守恒得:2mv。十mv。=5mv ①解得:v=vo ②对A用动能定理,有:一μmgS=mν2―m(2ν0)2 ③解得:S= ④木块B匀减速运动,加速度大小al=μg, ⑤木块C匀加速运动,加速度大小a2=μg, ⑥后来木块B与C一起匀加速,加速度大小a3=μg, ⑦从开始到木块B与木块C速度相等有:Vo一alt=a2t ⑧得到t=,vBC= ⑨木块B匀减速位移:S1=vot一alt2 = ⑩木块B与C一起匀加速位移:S2== (11)故AB至少间距:△S=S一(S1十S2)= (12)评分标准:本题满分20分。①式给3分,②式给1分,③式给3分,④式给1分,⑤、⑥、⑦、⑩、(11)、(12)式各给2分。

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
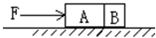 如图所示,质量为3m的光滑物体A与质量为m的光滑物体B,放在水平面上,在水平推力F从左向右的推力作用下加速运动,则A和B的相互作用力大小为
如图所示,质量为3m的光滑物体A与质量为m的光滑物体B,放在水平面上,在水平推力F从左向右的推力作用下加速运动,则A和B的相互作用力大小为 如图所示,质量为3m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平力F的作用下,A、B一起做匀加速直线运动,则二者的加速度为
如图所示,质量为3m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平力F的作用下,A、B一起做匀加速直线运动,则二者的加速度为
 (1)通过α粒子散射实验
(1)通过α粒子散射实验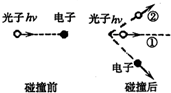 (1)如图所示为康普顿效应示意图,光子与一个静止的电子发生碰撞,图中标出了碰撞后电子的运动方向.设碰前光子频率为v,碰后为v′,则关于光子碰后的运动方向和频率的说法中正确的是
(1)如图所示为康普顿效应示意图,光子与一个静止的电子发生碰撞,图中标出了碰撞后电子的运动方向.设碰前光子频率为v,碰后为v′,则关于光子碰后的运动方向和频率的说法中正确的是