题目内容
如图所示，用面积为S的活塞在汽缸内封闭着一定质量的空气，活塞上放一砝码，活塞和砝码的总质量为m，现对汽缸缓缓加热使汽缸内的空气温度从T1升高到T2，且空气柱的高度增加了△l，已知加热时气体吸收的热量为Q，外界大气压强为p，问：①此过程中被封闭气体的内能变化了多少？②被封闭空气初始状态的体积．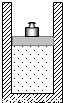
【答案】分析：①利用热力学第一定律判断气体的内能变化，判断的时候要注意做功W和热量Q的符号，对外做功和放热为负的，对气体做功和吸热为正的．
②气体做的是等压变化，根据盖-吕萨克定律计算即可．
解答：解：①由受力分析和做功分析知，在气体缓缓膨胀过程中，活塞与砝码的压力对气体做负功，大气压力对气体做负功，
根据热力学第一定律得
△U=W+Q=-mg△l-pS△l+Q
②被封闭气体等压变化，据盖-吕萨克定律得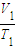
=
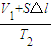
解得V1=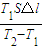
答：①此过程中被封闭气体的内能变化了-mg△l-pS△l+Q；
②被封闭空气初始状态的体积为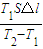
．
点评：以封闭的气体为研究对象，找出气体变化前后的状态参量，利用气体的状态方程计算即可．
②气体做的是等压变化，根据盖-吕萨克定律计算即可．
解答：解：①由受力分析和做功分析知，在气体缓缓膨胀过程中，活塞与砝码的压力对气体做负功，大气压力对气体做负功，
根据热力学第一定律得
△U=W+Q=-mg△l-pS△l+Q
②被封闭气体等压变化，据盖-吕萨克定律得
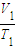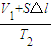
=解得V1=
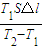
答：①此过程中被封闭气体的内能变化了-mg△l-pS△l+Q；
②被封闭空气初始状态的体积为
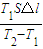．点评：以封闭的气体为研究对象，找出气体变化前后的状态参量，利用气体的状态方程计算即可．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
（1）在研究性学习的过程中，针对能源危机、大气污染等问题同学们提出如下四个活动方案，哪些从理论上讲是可行的
（2010?安丘市模拟）如图所示，用面积为S的活塞在汽缸内封闭着一定质量的空气，活塞上放一砝码，活塞和砝码的总质量为m，现对汽缸缓缓加热使汽缸内的空气温度从T1升高到T2，且空气柱的高度增加了△l，已知加热时气体吸收的热量为Q，外界大气压强为p0，问：①此过程中被封闭气体的内能变化了多少？②被封闭空气初始状态的体积．
