题目内容
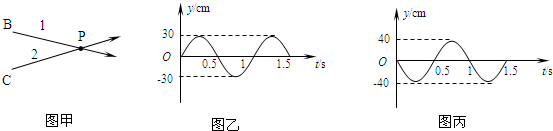
 如图,横波1沿BP方向传播,它在B点的振动方程为y1=30cos2πt(cm);横波2沿CP方向传播,它在C点的振动方程为y2=40cos(2πt+π)(cm).P与B相距40cm,P与C相距50cm,波速20cm/s.两横波在P处相遇,两横波振动方向相同,P点振幅为( )
如图,横波1沿BP方向传播,它在B点的振动方程为y1=30cos2πt(cm);横波2沿CP方向传播,它在C点的振动方程为y2=40cos(2πt+π)(cm).P与B相距40cm,P与C相距50cm,波速20cm/s.两横波在P处相遇,两横波振动方向相同,P点振幅为( )分析:由方程表达式可求出周期和振幅,由波速公式求出波长;根据P到B、C的路程差与波长的关系,分析P的振动是加强还是减弱,再研究P处相遇时,P点振幅.
解答:解:B点的振动方程为y1=30cos2πt(cm)与C点的振动方程为y2=40cos(2πt+π)(cm).可知,振动周期T=
=1s;
根据v=
可知,λ=vT=20×1cm=20cm.
PC-PB=40cm-30cm=10cm=0.5λ,而t=0时刻两波的振动方向相反,则P是振动加强的点,振幅等于两波振幅之和,即为70cm.故D正确,ABC错误.
故选D
| 2π |
| ω |
根据v=
| λ |
| T |
PC-PB=40cm-30cm=10cm=0.5λ,而t=0时刻两波的振动方向相反,则P是振动加强的点,振幅等于两波振幅之和,即为70cm.故D正确,ABC错误.
故选D
点评:本题的解题关键是掌握波的叠加原理进行分析,根据路程差和起振方向关系进行分析.

练习册系列答案
相关题目




 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求: