题目内容
【题目】质量为 1kg 的小球静止在水平地面上，小球在 F=14N 竖直向上的恒定外力作用下向上做匀加速直线运动， 运动过程中小球所受阻力大小恒定，方向与运动方向相反。
（1）小球运动 4s，上升 16m，求小球受到的阻力大小
（2）若小球运动 3s 后，外力消失，求小球落地时的速度大小
（3）在（2）问条件下，要使小球不落到地面上，则在外力消失多久后恢复外力。
【答案】(1)2N(2)
(3)
【解析】
(1)根据位移时间关系
，解得：
，根据牛顿第二定律可知：
解得：
。
(2) 若小球运动 3s 后，速度
上升位移
之后加速度
到达最高点时间
到达最高点的位移
之后下落，加速度
落地速度
(3)从最高点经过t时间施加外力，此时速度
，之后减速到零的时间
根据位移关系有
联立解得：
，所以经过
恢复外力。
答：(1)2N(2)(3)
练习册系列答案
相关题目
【题目】在“探究小车速度随时间变化的规律”的实验中,纸带记录了小车的运动情况,在纸带上确定出A、B、C、D、E、F共6个计数点,每两个相邻的计数点之间还有4个点未画出。x1=1.40 cm、x2=2.90 cm、x3=4.38 cm、x4=5.88 cm、x5=7.39 cm。
(1)试根据纸带上各个计数点间的距离,计算出打下B、E两个点时小车的瞬时速度,并将这两个速度值填入下表__________, __________。（结果保留3三位小数）
速度/(m·s-1) | vB | vC | vD | vE |
数值 | 0.364 | 0.513 |
(2)将B、C、D、E各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线_____________。
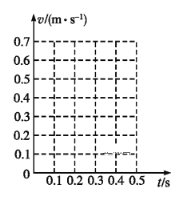
(3)由所画速度—时间图象求出小车的加速度为____ m/s2(保留三位有效数字)。
