题目内容
12.如图(a),木板OA可绕轴O在竖直平面内转动,木板上有一质量为m=1kg的物块,始终受到平行于斜面、大小为8N的力F的作用.改变木板倾角,在不同倾角时,物块会产生不同的加速度a,如图(b)所示为加速度a与斜面倾角的关系图线.已知物块与木板间的动摩擦因数为μ=0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力.求:(g取10m/s2,sin37?=0.6,cos37?=0.8)
(1)图线与纵坐标交点a0的大小;
(2)图线与θ轴重合区间为[θ1,θ2],木板处于该两个角度时的摩擦力指向何方?在斜面倾角处于θ1和θ2之间时,物块的运动状态如何?
(3)如果木板长L=2m,倾角为37°,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?
分析 (1)纵坐标交点表示木板水平放置时的加速度,根据牛顿第二定律即可求解;
(2)当摩擦力沿斜面向下且加速度为零时木板倾角为θ1,当摩擦力沿斜面向上且加速度为零时木板倾角为θ2,这时物块处于静止状态;
(3)根据牛顿第二定律分别求出有F和撤去F时的加速度,根据匀变速直线运动的基本公式求出这两个过程的位移,根据两段位移之和为L求解.
解答 解:(1)当木板水平放置时,物块的加速度为a0
此时滑动摩擦力 f=μN=μmg=0.2×1×10 N=2N
由牛顿第二定律F-f=ma0,
求得a0=$\frac{F-f}{m}=\frac{8-2}{1}$ m/s2=6m/s2
(2)当木板倾角为θ1时,摩擦力沿斜面向下
当木板倾角为θ2时,摩擦力沿斜面向上
当θ角处于θ1和θ2之间时物块静止
(3)力F作用间间最多时,撤去力后物块滑到斜面顶端时速度恰好减小到零.
设力F作用时物块的加速度为a1,由牛顿第二定律得
${a}_{1}=\frac{F-mgsin37°-μmgcos37°}{m}$=$\frac{8-10×0.6-0.2×10×0.8}{1}m/{s}^{2}=0.4m/{s}^{2}$.
撤去力F后物块的加速度大小为a2,由牛顿第二定律
${a}_{2}=\frac{mgsin37°+μmgcos37°}{m}$=$\frac{10×0.6+0.2×10×0.8}{1}m/{s}^{2}=7.6$m/s2
设物块不冲出木板顶端,力F最长作用时间为t
则撤去力F时的速度v=a1t
由题意有 $L={s}_{1}+{s}_{2}=\frac{1}{2}{a}_{1}{t}^{2}+\frac{{{a}_{1}}^{2}{t}^{2}}{2{a}_{2}}$.
由以上各式得 t=$\sqrt{\frac{2{a}_{2}L}{{a}_{1}({a}_{1}+{a}_{2})}}=\sqrt{\frac{2×7.6×2}{0.4×(0.4+7.6)}}s≈3.1s$.
答:(1)图线与纵坐标交点a0的大小为6m/s2;
(2)当木板倾角为θ1时,摩擦力沿斜面向下,当木板倾角为θ2时,摩擦力沿斜面向上,当θ角处于θ1和θ2之间时物块静止.
(3)为保证物块不冲出木板顶端,力F最多作用3.1s.
点评 本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们能根据图象得出有效信息,难度适中.


| A. | t2时刻物体的加速度最大 | B. | t2时刻摩擦力的功率最大 | ||
| C. | t3时刻物体的动能最大 | D. | t3时刻物体开始反向运动 |
| A. | 液体表面存在张力是因为液体表面层分子间的距离大于液体内部分子间的距离 | |
| B. | 温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同 | |
| C. | 在完全失重的情况下,密闭容器内的气体对器壁也有压强 | |
| D. | 晶体和非晶体在一定条件下可以相互转化 | |
| E. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在斥力的缘故 |
| A. | 1s | B. | 2s | C. | 3s | D. | 4s |

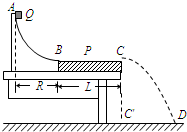 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的光滑四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的光滑四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下: 如图,xOy坐标系处于一匀强电场内,将一电量为-q的点电荷由A点分别移至x轴上的B点、C点,电场力做功均为W(W>0),此电场的场强方向为+y方向.若在恒定外力作用下使电荷沿AB做直线运动,A点坐标为(d,d),∠ABC=60°,则此外力的最小值为$\frac{W}{2d}$.
如图,xOy坐标系处于一匀强电场内,将一电量为-q的点电荷由A点分别移至x轴上的B点、C点,电场力做功均为W(W>0),此电场的场强方向为+y方向.若在恒定外力作用下使电荷沿AB做直线运动,A点坐标为(d,d),∠ABC=60°,则此外力的最小值为$\frac{W}{2d}$.
 某同学做研究平抛物体运动的实验时,不慎未定好原点,只画了竖直线,而且只描出了平抛物体的后一部分轨迹,如图所示,依此图加一把刻度尺,如何计算出平抛物体的初速度v0?
某同学做研究平抛物体运动的实验时,不慎未定好原点,只画了竖直线,而且只描出了平抛物体的后一部分轨迹,如图所示,依此图加一把刻度尺,如何计算出平抛物体的初速度v0?