题目内容
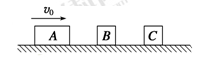
光滑水平轨道上有三个木块A、B、C，质量分别为mA=3m、mB=mC=m，开始时B、C均静止，A以初速度νo向右运动，A与B相撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变．求B与C碰撞前B的速度大小．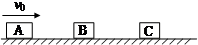
【答案】分析：A与B相撞，B又与C发生碰撞，根据动量守恒定律列出等式求解．
解答：解：设A与B碰撞后，A的速度为vA，B与C碰撞前B的速度为vB，B与C碰撞后粘在一起的速度为v，由动量守恒定律得
对A、B木块：mAv=mAvA+mBvB…①
对B、C木块：mBvB=（mB+mC）v… ②
由A与B间的距离保持不变可知
vA=v… ③
联立①②③式，代入数据得vB=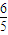
v
答：B与C碰撞前B的速度大小是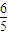
v．
点评：本题分两个物理过程研究：A与B相撞，B又与C发生碰撞的过程，基本的思路是动量守恒应用．
解答：解：设A与B碰撞后，A的速度为vA，B与C碰撞前B的速度为vB，B与C碰撞后粘在一起的速度为v，由动量守恒定律得
对A、B木块：mAv=mAvA+mBvB…①
对B、C木块：mBvB=（mB+mC）v… ②
由A与B间的距离保持不变可知
vA=v… ③
联立①②③式，代入数据得vB=
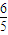v答：B与C碰撞前B的速度大小是
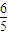v．点评：本题分两个物理过程研究：A与B相撞，B又与C发生碰撞的过程，基本的思路是动量守恒应用．
练习册系列答案
名校课堂系列答案
相关题目
（2011?海淀区模拟）如图所示，在足够长的光滑水平轨道上有三个小木块A、B、C，质量分别为mA、mB、mC，且mA=mB=1.0kg，mC=2.0kg，其中B与C用一个轻弹簧拴接在一起，开始时整个装置处于静止状态．A和B之间有少许塑胶炸药，A的左边有一个弹性挡板．现在引爆塑胶炸药，若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能，A和B分开后，A恰好在B、C之间的弹簧第一次恢复到原长时追上B，并且与B发生碰撞后粘在一起．忽略小木块和弹性挡板碰撞过程中的能量损失．求：
、
，开始时B、C均静止，A以初速度向右运动，A与B相撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变。求B与C碰撞前B的速度大小。
