题目内容
4.某次在“探究弹簧伸长量与弹力的关系,并测定弹簧的劲度系数”实验中,实验装置如图甲所示.实验所用的每个钩码的质量均为m.实验时先测出弹簧的自然长度,然后将8个钩码逐个挂在绳子的下端,并测出相应的弹簧总长度,然后算出相应的弹簧伸长量x.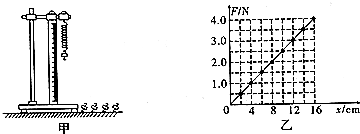
(1)下列有关本实验的要求,正确的是ABD(填序号).
A.同时挂上8个钩码不能超过弹簧的弹性限度
B.在安装刻度尺时,必须使刻度尺保持与弹簧的轴线平行
C.将弹簧水平放置,然后测量其“自然长度”
D.将弹簧竖直悬挂不挂钩码,然后测量其“自然长度”
(2)通过上述实验,将测得的8组数据描点在F-x坐标图中,并作出如图乙所示的弹力大小F与弹簧伸长量x的关系图线.由此图线可得该弹簧的劲度系数k=25N/m.
(3)若当地的重力加速度g取l0m/s2,则由上述F-x的关系图象可知,本实验所使用的钩码质量m为50g.
分析 (1)弹簧是竖直的,要减小误差,刻度尺必须竖直,在操作过程中,不能超过弹簧的劲度系数;
(2)弹簧处于原长时,弹力为零;根据胡克定律F=k△x求解劲度系数
解答 解:(1)在探究弹簧的弹力与伸长量的关系式,必须满足不能超过弹簧的弹性限度,故A正确;
B、在安装刻度尺时,必须使刻度尺保持与弹簧的轴线平行,读数才准确,故B正确;
CD、将弹簧竖直悬挂不挂钩码,然后测量其“自然长度“,故C错误,D正确
故选:ABD
(2)在F-x图象中,斜率代表弹簧的劲度系数,k=$\frac{F}{△x}=\frac{4.0}{0.16}N/m=25N/m$
(3)8个钩码的重力为4N,根据F=8mg解得m=$\frac{F}{8g}=\frac{4}{80}kg=50g$
故答案为:(1)ABD;(2)25;(3)50
点评 本题关键是明确实验原理,然后根据胡克定律F=k△x并结合图象列式求解,不难.

练习册系列答案
相关题目
19.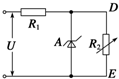 如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )
如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )
 如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )
如图所示,A为一稳压管,它的作用是保证DE两端的电压UDE恒定不变,当流过稳压管的电流在20mA和80mA之间时,UDE就稳定在10V,R2为一可变电阻,它的最小值为500Ω,最大值为无穷大(即断路).设电源电压U=20V,则当R2变化时,为使UDE稳定在10V,R1可取下列几个电阻值中的( )| A. | 100Ω | B. | 200Ω | C. | 300Ω | D. | 4 000Ω |
9.如图所示,电源电动势为E,内阻为r,当电建K闭合时,各电表示数变化为( )


| A. | A1变小,A2变大,V1变小,V2变大 | B. | A1变大,A2变小,V1变大,V2变小 | ||
| C. | A1变小,A2变大,V1变小,V2变大 | D. | A1变大,A2变小,V1变大,V2变大 |
16. 如图所示,一质量为m的小物体以一定的速率v0滑到水平传送带上左端的A点,当传送带始终静止时,已知物体能滑过右端的B点,则下列判断正确的是( )
如图所示,一质量为m的小物体以一定的速率v0滑到水平传送带上左端的A点,当传送带始终静止时,已知物体能滑过右端的B点,则下列判断正确的是( )
 如图所示,一质量为m的小物体以一定的速率v0滑到水平传送带上左端的A点,当传送带始终静止时,已知物体能滑过右端的B点,则下列判断正确的是( )
如图所示,一质量为m的小物体以一定的速率v0滑到水平传送带上左端的A点,当传送带始终静止时,已知物体能滑过右端的B点,则下列判断正确的是( )| A. | 传送带若逆时针方向运行,物体一定也能滑过B点 | |
| B. | 传送带若逆时针方向运行,物体可能先向右做匀减速运动直到速度减为零,然后向左加速,不滑过B点 | |
| C. | 传道带若顺时针方向运行,物体将一直做匀速运动滑过B点 | |
| D. | 传送带若顺时针方向运行,当其运行速率(保持不变)v>v0时,物体一定向右一直做匀加速运动滑过B点 |
14.一个作匀加速直线运动的物体,通过A点的瞬时速度是vl,通过B点的瞬时速度是v2,下列说法正确的是( )
| A. | A到B的平均速度为$\overline v$=$\frac{{{v_1}+{v_2}}}{2}$ | |
| B. | A到B中点的速度为${v_{\frac{x}{2}}}=\sqrt{\frac{{{v_2}^2+{v_1}^2}}{2}}$ | |
| C. | $\overline v$>${v_{\frac{x}{2}}}$ | |
| D. | A到B中间时刻的速度为 ${v_{\frac{t}{2}}}>{v_{\frac{x}{2}}}$ |
 如图所示,铜棒ab长L=0.3m,质量为m=9×10-2kg,两端与长为s=1m的轻铜线相连,整个装置处在竖直向下的匀强磁场中,磁感强度B=1T.铜棒中保持有恒定电流通过时,铜棒稳定后的偏转角为30°.求:
如图所示,铜棒ab长L=0.3m,质量为m=9×10-2kg,两端与长为s=1m的轻铜线相连,整个装置处在竖直向下的匀强磁场中,磁感强度B=1T.铜棒中保持有恒定电流通过时,铜棒稳定后的偏转角为30°.求: 小红利用如图甲所示的电路探究“电流与电阻的关系”.已知电源电压为6V且保持不变,有三种规格滑动变阻器可供选择:0~40Ω,0~30Ω,0~20Ω,用到的电阻R的阻值分别为25Ω、20Ω、15Ω、10Ω、5Ω,实验中控制电阻R两端的电压为2.5V不变.
小红利用如图甲所示的电路探究“电流与电阻的关系”.已知电源电压为6V且保持不变,有三种规格滑动变阻器可供选择:0~40Ω,0~30Ω,0~20Ω,用到的电阻R的阻值分别为25Ω、20Ω、15Ω、10Ω、5Ω,实验中控制电阻R两端的电压为2.5V不变.
 如图所示,半径R=2.5m的光滑半圆形轨道固定在水平地面上,一小球以某一速度从半圆形轨道的最低点A冲上轨道,从半圆轨道的最高点B水平飞出,小球在B点时对轨道的压力恰好等于小球受到的重力.不计空气阻力,重力加速度g=10m/s2.求:
如图所示,半径R=2.5m的光滑半圆形轨道固定在水平地面上,一小球以某一速度从半圆形轨道的最低点A冲上轨道,从半圆轨道的最高点B水平飞出,小球在B点时对轨道的压力恰好等于小球受到的重力.不计空气阻力,重力加速度g=10m/s2.求: