题目内容
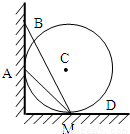 如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心.已知在同一时刻:a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点;则( )
如图所示,位于竖直平面内的固定光滑圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M的连线和水平面的夹角为60°,C是圆环轨道的圆心.已知在同一时刻:a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点;c球由C点自由下落到M点;则( )A.a球最先到达M点
B.b球最先到达M点
C.c球最先到达M点
D.b球和c球都可能最先到达M点
【答案】分析:根据几何关系分别求出各个轨道的位移,根据牛顿第二定律求出加速度,再根据匀变速直线运动的位移时间公式求出运动的时间,从而比较出到达M点的先后顺序.
解答:解:对于AM段,位移 ,加速度
,加速度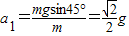 ,根据
,根据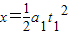 得,
得,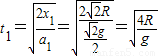 .
.
对于BM段,位移x2=2R,加速度 ,由
,由 得,
得, .
.
对于CM段,位移x3=R,加速度a3=g,由 得,
得, .知t3最小,故C正确,A、B、D错误.
.知t3最小,故C正确,A、B、D错误.
故选C.
点评:解决本题的关键根据牛顿第二定律求出各段的加速度,运用匀变速直线运动的位移时间公式进行求解.
解答:解:对于AM段,位移
 ,加速度
,加速度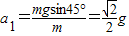 ,根据
,根据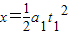 得,
得,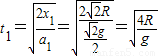 .
.对于BM段,位移x2=2R,加速度
 ,由
,由 得,
得, .
.对于CM段,位移x3=R,加速度a3=g,由
 得,
得, .知t3最小,故C正确,A、B、D错误.
.知t3最小,故C正确,A、B、D错误.故选C.
点评:解决本题的关键根据牛顿第二定律求出各段的加速度,运用匀变速直线运动的位移时间公式进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H,质量为m的小球从A点静止释放(球达B点水平速度大小等于球由O点自由释放至B点速度大小),最后落在地面C处,不计空气阻力,( g=10m/s2)求:
如图所示,位于竖直平面上的1/4圆弧光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H,质量为m的小球从A点静止释放(球达B点水平速度大小等于球由O点自由释放至B点速度大小),最后落在地面C处,不计空气阻力,( g=10m/s2)求: 如图所示,位于竖直平面上的
如图所示,位于竖直平面上的 如图所示,位于竖直平面上的
如图所示,位于竖直平面上的