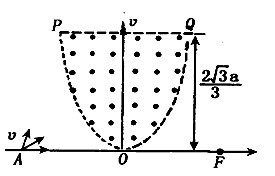
题目内容
 磁聚焦被广泛的应用在电真空器件中,如图所示,在坐标xoy中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
磁聚焦被广泛的应用在电真空器件中,如图所示,在坐标xoy中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为2
| ||
| 3 |
| x(a-x) | ||||
|
(1)匀强磁场的磁感应强度;
(2)粒子射入磁场时的速度方向与x轴的夹角为多大时,粒子在磁场中运动时间最长,最长对间为多少?
分析:先根据三角形相似求出横坐标x与y的比例关系,然后根据洛伦兹力提供向心力列方程求出B;
先求出所用时间t的表达式,根据根据数学知识求最大值.
先求出所用时间t的表达式,根据根据数学知识求最大值.
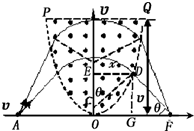
解答:解:(1)设磁场的磁感应强度为B,粒子在磁场中做圆周运动的半径为r,圆心为C,从D处射出磁场,其坐标为(x,y),因Rt△CED相似于Rt△DGF
可得
=
且POQ的曲线方程为y=
解得:r=
a
因 r=
解得:B=
(2)设粒子射入磁场时的速度方向与x轴夹角为θ时,粒子在磁场中运动的轨迹与PQ相切,则运动的时间最长,最长时间为t,由几何知识得
=r+y-rcosθ x=rsinθ
解得:sinθ=
θ=60°=
且 t=
解得:t=
=
答:(1)匀强磁场的磁感应强度为
;
(2)粒子射入磁场时的速度方向与x轴的夹角为
时,粒子在磁场中运动时间最长,最长对间为
.
可得
| y |
| x |
| a-x | ||
|
且POQ的曲线方程为y=
| x(a-x) | ||||
|

解得:r=
| ||
| 3 |
因 r=
| mv |
| qB |
解得:B=
| ||
| aq |
(2)设粒子射入磁场时的速度方向与x轴夹角为θ时,粒子在磁场中运动的轨迹与PQ相切,则运动的时间最长,最长时间为t,由几何知识得
2
| ||
| 3 |
解得:sinθ=
| ||
| 2 |
| π |
| 3 |
且 t=
| αm |
| qB |
解得:t=
| 2θm |
| qB |
2
| ||
| 9v |
答:(1)匀强磁场的磁感应强度为
| ||
| qa |
(2)粒子射入磁场时的速度方向与x轴的夹角为
| π |
| 3 |
2
| ||
| 9v |
点评:本题用到的数学方法较多,一定要注重数学方法在物理中的应用,特别在带电粒子在磁场中的偏转中一定要注意几何关系的正确应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
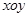 中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为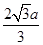 ,边界POQ的曲线方程为
,边界POQ的曲线方程为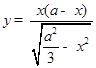 。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:
。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求: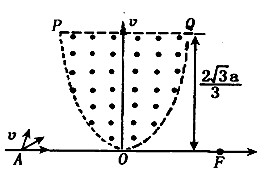
 中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为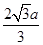 ,边界POQ的曲线方程为
,边界POQ的曲线方程为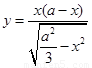 。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:
。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求: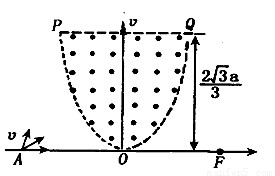
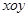 中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为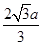 ,边界POQ的曲线方程为
,边界POQ的曲线方程为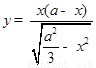 。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:
。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求: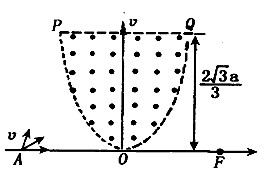
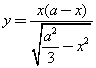 。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:
。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求: