题目内容
如图所示，木块B上表面是水平的，当木块A置于B上，并与B保持相对静止，一起沿固定的光滑斜面由静止开始下滑，在下滑过程中（ ）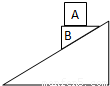
A．A所受的合外力对A不做功
B．B对A做正功
C．B对A的摩擦力做负功
D．A对B不做功
【答案】分析：分析两物体的受力及运动，由功的公式可分析各力对物体是否做功，根据夹角可判功的正负．
解答：解：A、木块向下加速运动，故动能增加，由动能定理可知，木块m所受合外力对m做正功，故A错误；
B、A、B整体具有沿斜面向下的加速度，设为a，将a正交分解为竖直方向分量a1，水平分量a2，如图所示，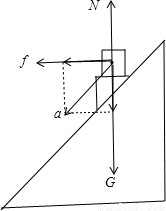
由于具有水平分量a2，故必受水平向右摩擦力f，A受力如图所示，所以支持力做负功，摩擦力做正功，故C错；
由牛顿第二定律得；竖直方向上； mg-N=ma1 ①
水平方向上：f=ma2 ②
假设斜面与水平方向的夹角为θ，摩擦力与弹力的合力与水平方向夹角为α，由几何关系得；
a1=gsinθsinθ ③
a2=gsinθcosθ ④
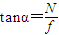⑤
①→⑤联立得：
=
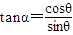
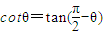
即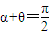
所以B对A的作用力与斜面垂直，所以B对A不做功，故B错误；
由牛顿第三定律得，A对B的作用力垂直斜面向下，所以A对B也不做功，故D正确．
故选D．
点评：判断外力是否做功及功的正负可根据做功的条件是否做功，再根据力与位移方向的夹角判断功的正负，也可以根据力与速度方向的夹角判断功的正负．
解答：解：A、木块向下加速运动，故动能增加，由动能定理可知，木块m所受合外力对m做正功，故A错误；
B、A、B整体具有沿斜面向下的加速度，设为a，将a正交分解为竖直方向分量a1，水平分量a2，如图所示，
由于具有水平分量a2，故必受水平向右摩擦力f，A受力如图所示，所以支持力做负功，摩擦力做正功，故C错；
由牛顿第二定律得；竖直方向上； mg-N=ma1 ①
水平方向上：f=ma2 ②
假设斜面与水平方向的夹角为θ，摩擦力与弹力的合力与水平方向夹角为α，由几何关系得；
a1=gsinθsinθ ③
a2=gsinθcosθ ④
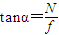⑤①→⑤联立得：
=
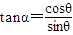
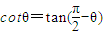
即
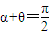所以B对A的作用力与斜面垂直，所以B对A不做功，故B错误；由牛顿第三定律得，A对B的作用力垂直斜面向下，所以A对B也不做功，故D正确．
故选D．
点评：判断外力是否做功及功的正负可根据做功的条件是否做功，再根据力与位移方向的夹角判断功的正负，也可以根据力与速度方向的夹角判断功的正负．
练习册系列答案
相关题目
某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系，实验室提供如下器材：
在研究摩擦力的实验中，用轻质弹簧秤沿水平方向拉一置于水平桌面上的木块，木块与桌面间的动摩擦因数处处相同，如图所示．木块运动状态及弹簧秤的读数如下表所示，则由表可知，在所测得五组数据中，下列说法正确的是：（ ）| 实验记录次数 | 小木块运动状态 | 弹簧秤读数（N） |
| 1 | 静止 | 0.2 |
| 2 | 静止 | 0.5 |
| 3 | 加速 | 0.7 |
| 4 | 匀速 | 0.5 |
| 5 | 减速 | 0.3 |
| A、其中有两组摩擦力大小相同 |
| B、其中有三组摩擦力大小相同 |
| C、其中有四组摩擦力大小相同 |
| D、其中五组摩擦力大小都相同 |
