题目内容
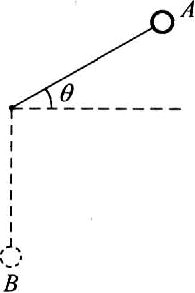
 如图所示,在一根不可伸长的细线上系一个质量为m的小球,当把小球拉到使细线与水平面成θ=30°角时,轻轻释放小球.不计空气阻力,求小球落到悬点正下方的B点时对细线的拉力.
如图所示,在一根不可伸长的细线上系一个质量为m的小球,当把小球拉到使细线与水平面成θ=30°角时,轻轻释放小球.不计空气阻力,求小球落到悬点正下方的B点时对细线的拉力.分析:小球先自由落体运动,当细线刚伸直时,沿细线方向速度突然减为零,沿切线方向速度不变,之后根据机械能守恒定律求最低点速度,最后在最低点根据合力提供向心力列式求解.
解答:解: 如图所示,当小球下落到C点,细绳偏下与水平成θ角,细绳张紧,小球速度
如图所示,当小球下落到C点,细绳偏下与水平成θ角,细绳张紧,小球速度
v=
=
.
v垂直于细绳方向的分量
v1=vcosθ=
.
从C到B,机械能守恒,设到B点时的速度为vB
则
m
=
m
+mg(l-lsinθ)
得
F合=
=
+2mg(1-sinθ)=
(
)2+2mg(1-sinθ)=
mg.
在B点应用牛顿第二定律
T-mg=
解得
T=mg+
=mg+
mg=
mg
即小球落到悬点正下方的B点时对细线的拉力为
mg.
 如图所示,当小球下落到C点,细绳偏下与水平成θ角,细绳张紧,小球速度
如图所示,当小球下落到C点,细绳偏下与水平成θ角,细绳张紧,小球速度v=
| 2g?2lsinθ |
| 2gl |
v垂直于细绳方向的分量
v1=vcosθ=
| ||
| 2 |
| 2gl |
从C到B,机械能守恒,设到B点时的速度为vB
则
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 1 |
得
F合=
m
| ||
| l |
m
| ||
| l |
| m |
| l |
| ||
| 2 |
| 2gl |
| 5 |
| 2 |
在B点应用牛顿第二定律
T-mg=
m
| ||
| l |
解得
T=mg+
m
| ||
| l |
| 5 |
| 2 |
| 7 |
| 2 |
即小球落到悬点正下方的B点时对细线的拉力为
| 7 |
| 2 |
点评:本题关键是先分析清楚小球的运动情况,然后根据运动学公式、速度分解法则、机械能守恒定律和向心力公式列式求解.

练习册系列答案
相关题目