题目内容
（B组） 质量为
m的猎狗，拉着质量为m的雪撬，在水平冰面上做匀速圆周运动，其府视图如下图所示，猎狗和雪撬（均可视为质点）的运动轨迹分别是图中的内圆和外圆．已知长为L的绳沿水平方向且与内圆相切，雪撬的轨道半径为2L，测出猎狗运动一周所用时间为T，求：（1）雪撬的线速度的大小．（2）绳中张力F和雪撬与冰面之间的动摩擦因数μ．（3）地面对猎狗的摩擦力大小f．
| 3 |
（1）雪橇做匀速圆周运动，周期为T，因而，线速度为v=
=
=
；
故雪撬的线速度的大小为
．
（2）对雪橇受力分析，受重力、支持力，水平面内（如图）受绳子的拉力F、向后的摩擦力f′，将拉力F沿半径方向和切线方向正交分解，根据牛顿第二定律，有：
Fsin30°=m（
）2（2L） ①；
Fcos30°=f′②；
由①式得：F=
③；
故雪撬与冰面之间的动摩擦因数μ=
=
；
故绳中张力F为
，雪撬与冰面之间的动摩擦因数μ为
．
（3）对猎狗受力分析，除竖直方向的重力与支持力二力平衡外，水平面内还受绳子拉力F、摩擦力f，将f沿着半径方向和切线方向正交分解，f1与F平衡，f2等于合力，提供向心力，如图；
根据牛顿第二定律，有：
f1=F=
④；
f2=
m（
）2
L=
⑤；
由第④、⑤两式可得，f=
=
；
故地面对猎狗的摩擦力大小为
．
| 2π r1 |
| T |
| 2π (2L) |
| T |
| 4πL |
| T |
故雪撬的线速度的大小为
| 4πL |
| T |
（2）对雪橇受力分析，受重力、支持力，水平面内（如图）受绳子的拉力F、向后的摩擦力f′，将拉力F沿半径方向和切线方向正交分解，根据牛顿第二定律，有：
Fsin30°=m（
| 2π |
| T |
Fcos30°=f′②；
由①式得：F=
| 16π2mL |
| T2 |
故雪撬与冰面之间的动摩擦因数μ=
| f′ |
| mg |
8
| ||
| gT2 |
故绳中张力F为
| 16π2mL |
| T2 |
8
| ||
| gT2 |
（3）对猎狗受力分析，除竖直方向的重力与支持力二力平衡外，水平面内还受绳子拉力F、摩擦力f，将f沿着半径方向和切线方向正交分解，f1与F平衡，f2等于合力，提供向心力，如图；
根据牛顿第二定律，有：
f1=F=
| 16π2mL |
| T2 |
f2=
| 3 |
| 2π |
| T |
| 3 |
| 12π2mL |
| T2 |
由第④、⑤两式可得，f=
|
| 20π2mL |
| T2 |
故地面对猎狗的摩擦力大小为
| 20π2mL |
| T2 |
练习册系列答案
相关题目
（B组） 质量为
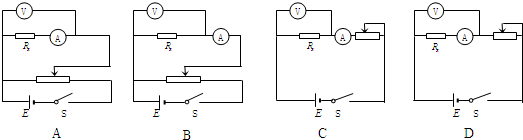
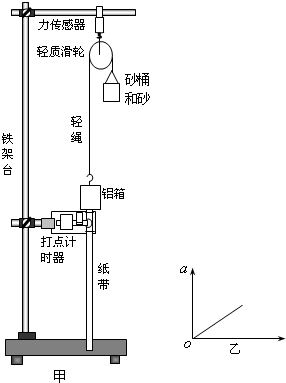
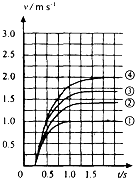（2006?广州二模）从高空下落的雨点打在人身上并不可怕，说明其速度不会很大；一位同学猜想这可能是由于运动物体受空气阻力的大小与其速度有关，于是定下了“在其他条件相同的情况下，运动物体所受空气阻力与运动速度关系”的研究课题，实验设计方案和实验过程如下．
一个带电粒子只在电场力作用下通过匀强电场中的a、b两点，一组平行的带箭头的实线表示匀强电场的电场线，如图所示．已知带电粒子通过a、b两点的速度大小分别是5m/s和3m/s，粒子的质量是100g，a、b两点的电势差为80V．