题目内容
 (2006?河东区二模)如图所示,BC两物体静止在足够长的光滑水平面上,两者之间有一被压缩的短弹簧,弹簧与B连接,与C不连接,别一物体A沿水平面以v0=5m/s的速度向右运动.现烧断用于压缩弹簧的细线,将C物体向左弹射出去,C与A碰撞后粘合在一起,已知A、B、C三物体的质量分别为 mA=mB=2kg,mc=1kg.为了使C与B不会再发生碰撞,则:
(2006?河东区二模)如图所示,BC两物体静止在足够长的光滑水平面上,两者之间有一被压缩的短弹簧,弹簧与B连接,与C不连接,别一物体A沿水平面以v0=5m/s的速度向右运动.现烧断用于压缩弹簧的细线,将C物体向左弹射出去,C与A碰撞后粘合在一起,已知A、B、C三物体的质量分别为 mA=mB=2kg,mc=1kg.为了使C与B不会再发生碰撞,则:(1)C物体的弹射速度至少为多大?
(2)在细线未烧断前,弹簧储存的弹性势能至少为多少?
分析:(1)系统动量守恒,由动量守恒定律可以求出C的速度;
(2)由能量守恒定律可以求出弹簧的弹性势能.
(2)由能量守恒定律可以求出弹簧的弹性势能.
解答:解:(1)以向右为正方向,B、C弹开时动量守恒:0=mCvC+mBvB ①,
A与C相碰动量守恒 mAvA-mCvC=(mC+mA)v ②,
若C不再与B相碰,则有 v=vB ③,
联立①②③三方程解得:vB=
=
m/s=2m/s,
vC=
=
m/s=4m/s;
(2)由能量守恒定律得:弹性势能:EP=
mBvB2+
mCvC2=12J;
答:(1)C物体的弹射速度至少为4m/s.
(2)在细线未烧断前,弹簧储存的弹性势能至少为12J.
A与C相碰动量守恒 mAvA-mCvC=(mC+mA)v ②,
若C不再与B相碰,则有 v=vB ③,
联立①②③三方程解得:vB=
| mAv0 |
| mA+mB+mC |
| 2×5 |
| 2+2+1 |
vC=
| mBvB |
| mC |
| 2×2 |
| 1 |
(2)由能量守恒定律得:弹性势能:EP=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)C物体的弹射速度至少为4m/s.
(2)在细线未烧断前,弹簧储存的弹性势能至少为12J.
点评:应用动量守恒定律与能量守恒定律即可正确解题,应用动量守恒定律解题时,要注意过程的选择与研究对象的选择.

练习册系列答案
相关题目
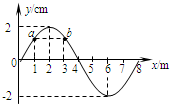 (2006?河东区二模)如图所示,一列简谐波以8.0m/s的速度传播,某一时刻波上有ab两质点,位移大小相等,方向相同,以下说法正确的是( )
(2006?河东区二模)如图所示,一列简谐波以8.0m/s的速度传播,某一时刻波上有ab两质点,位移大小相等,方向相同,以下说法正确的是( )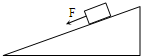 (2006?河东区二模)物体恰能在一个斜面上沿斜面匀速下滑,可以证明出此时斜面不受地面的摩擦力作用,若沿斜面方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力和地面的支持力,下列说法正确的是( )
(2006?河东区二模)物体恰能在一个斜面上沿斜面匀速下滑,可以证明出此时斜面不受地面的摩擦力作用,若沿斜面方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力和地面的支持力,下列说法正确的是( ) (2006?河东区二模)如图所示的一个匝数为10匝的矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动,周期为T,若用交流电压表测得a、b两点间的电压为20.0V,则可知:若从中性面开始计时,当t=
(2006?河东区二模)如图所示的一个匝数为10匝的矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动,周期为T,若用交流电压表测得a、b两点间的电压为20.0V,则可知:若从中性面开始计时,当t=