题目内容
17. 细线一端拴一个小球,另一端固定.设法使小球在水平面内做匀速圆周运动,如图所示.细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求:
细线一端拴一个小球,另一端固定.设法使小球在水平面内做匀速圆周运动,如图所示.细线与竖直方向夹角为θ,线长为L,小球质量为m,重力加速度为g.求:(1)绳子对小球的拉力的大小
(2)小球运动的向心加速度大小
(3)小球运动的线速度大小.
分析 (1)小球在水平面内做匀速圆周运动,对小球受力分析,根据合力提供向心力求出细线拉力的大小.
(2)根据向心力公式结合几何关系求出向心加速度;
(3)由向心力公式得:mgtanθ=$m\frac{{v}^{2}}{r}$求解线速度大小.
解答 解:(1)小球在水平面内做匀速圆周运动,对小球受力分析,如图
小球受重力、和绳子的拉力,合力提供向心力,根据几何关系可知:T=$\frac{mg}{cosθ}$
(2)由向心力公式得:mgtanθ=ma,
解得:a=gtanθ
(3)由向心力公式得:mgtanθ=$m\frac{{v}^{2}}{r}$,又 r=Lsinθ
解得:$v=\sqrt{gLtanθsinθ}$答:
(1)细线的拉力是$\frac{mg}{cosθ}$;
(2)小球运动的向心加速度大小为gtanθ;
(3)小球运动的线速度大小为$\sqrt{gLtanθsinθ}$.
点评 本题是圆锥摆问题,关键是分析受力情况,确定向心力的来源.要注意小球圆周运动的半径不等于绳长,难度不大,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
8. 单匝矩形线圈在磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,由O~D过程中( )
单匝矩形线圈在磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,由O~D过程中( )
 单匝矩形线圈在磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,由O~D过程中( )
单匝矩形线圈在磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,由O~D过程中( )| A. | 线圈中O时刻感应电动势最大 | |
| B. | 线圈中D时刻感应电动势为零 | |
| C. | 线圈中D时刻感应电动势最大 | |
| D. | 线圈O至D时刻平均感应电动势0.20 V |
5.在《探究加速度与力、质量的关系》实验中,某同学在某次实验时释放小车的瞬间装置状态如图1.
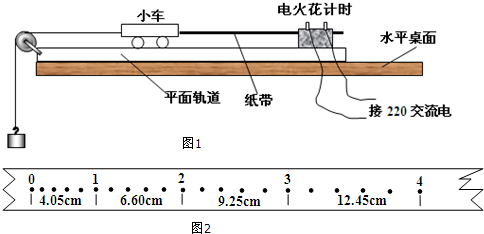
(Ⅰ)则操作中有待改进的是:①小车离计时器太远;②需平衡摩擦力
(Ⅱ)如图2为改进实验操作后某次实验打下的纸带数据,相邻两计数点间距如图所示,则该次实验加速度为2.76m/s2(保留3位有效数字)
(Ⅲ)若均使用同一规格钩码以改变小车总质量和悬挂重物的总重力,某同学得到多次运动中对应加速度,实验数据如表格所示
请选择一组数据用来研究加速度与力关系,并在答题卡坐标纸上作出相应图线.
作图要求:(1)完善坐标物理量及合理的物理量标度
(2)在坐标纸上标出所选数据,完成图线并标出数据坐标值;
(3)就你所选实验数据得到的结论做出评价.

(Ⅰ)则操作中有待改进的是:①小车离计时器太远;②需平衡摩擦力
(Ⅱ)如图2为改进实验操作后某次实验打下的纸带数据,相邻两计数点间距如图所示,则该次实验加速度为2.76m/s2(保留3位有效数字)
(Ⅲ)若均使用同一规格钩码以改变小车总质量和悬挂重物的总重力,某同学得到多次运动中对应加速度,实验数据如表格所示
| 小车钩码数 最悬挂钩码数 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1.39m/s2 | 1.16m/s2 | 1.00m/s2 | 0.94m/s2 | 0.78m/s2 |
| 2 | 2.48m/s2 | 2.20m/s2 | 2.00m/s2 | 1.81m/s2 | / |
| 3 | 3.38m/s2 | 2.89m/s2 | 2.76m/s2 | / | / |
| 4 | 4.15m/s2 | 3.68m/s2 | / | / | / |
| 5 | 4.59m/s2 | / | / | / | / |
作图要求:(1)完善坐标物理量及合理的物理量标度
(2)在坐标纸上标出所选数据,完成图线并标出数据坐标值;
(3)就你所选实验数据得到的结论做出评价.
12.在地球表面不同纬度的物体,因随地球自转而做匀速圆周运动,下列说法中正确的是( )
| A. | 这些物体运动的角速度相同 | B. | 这些物体运动的线速度相同 | ||
| C. | 这些物体运动向心加速度相同 | D. | 这些物体运动的线速度大小相等 |
6.利用如图1所示的装置测量滑块与水平长木板之间的动摩擦因数μ,一滑块放在水平长木扳上,左侧挂有一细软线,跨过固定在长木板边缘的定滑轮与一重物相连,在重物的牵引下,滑块在长木板上向左运动,重物落地后,滑块继续向左做匀减速运动,在长木板上安装有两个光电门,其中光电门甲固定在长木板的右侧,光电门乙的位置可移动,当一带有挡光片的滑块从右端向左端滑动时,与两个光电门都相连的计时器可以显示出挡光片从光电门甲至乙所用的时间t,每次都使滑块从同一点由静止开始运动,且滑块开始的位置到光电门甲之间的距离与重物开始的位置到地面的距离相等均为L,改变光电门乙到光电门甲之间的距离X,进行多次测量,并用米尺测量出光电门甲、乙之间相应的距离X,记下相应的t值,所得数据如表所示.
请你根据题目所给数据完成下列问题(g=9.8m/s2,结果保留两位有效数字):

(1)根据表中所给的数据,在图2的坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2;
(3)滑块与水平长木板之间的动摩擦因数=0.31.
| X(m) | 0.200 | 0.400 | 0.600 | 0.700 | 0.900 | 0.900 |
| t(s) | 0.088 | 0.189 | 0.311 | 0.385 | 0.473 | 0.600 |
| $\frac{X}{t}$(m/s) | 2.27 | 2.12 | 1.93 | 1.82 | 1.69 | 1.50 |

(1)根据表中所给的数据,在图2的坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2;
(3)滑块与水平长木板之间的动摩擦因数=0.31.
7. 如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
 如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )
如图所示是用光照射某种金属时逸出的光电子的最大初动能随入射光频率的变化图线(直线与横轴的交点坐标为4.27,与纵轴交点坐标为0.5).由图可知( )| A. | 该图线的斜率为$\frac{h}{e}$(h为普朗克常量,e为元电荷量) | |
| B. | 该金属的逸出功为0.5 eV | |
| C. | 该金属的截止频率为5.5×1014Hz | |
| D. | 该金属的截止频率为4.27×1014Hz |
 如图所示,A、B两物体通过一柔软且不可以伸长的软绳连接,跨在光滑小滑轮两侧,软绳与水瓶接触面平行,已知A、B两物体的质量为m,且可视为质点,软绳质量也为m,长为2L,平台离地面高围殴L,不计运动过程中的一切摩擦.初软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.
如图所示,A、B两物体通过一柔软且不可以伸长的软绳连接,跨在光滑小滑轮两侧,软绳与水瓶接触面平行,已知A、B两物体的质量为m,且可视为质点,软绳质量也为m,长为2L,平台离地面高围殴L,不计运动过程中的一切摩擦.初软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹. 如图所示,相距为L的两条足够长的光滑平行金属导轨固定在水平面上,导轨由两种材料组成.PG右侧部分单位长度电阻为r0,且PQ=QH=GH=L.PG左侧导轨电阻不计,导体棒AC的电阻为R0,整个导轨处于匀强磁场中,磁场方向垂直于导轨平面向下,磁感应强度大小为B.质量为m的导体棒AC在恒力F作用下从静止开始运动,在到达PG之前导体棒AC已经匀速.
如图所示,相距为L的两条足够长的光滑平行金属导轨固定在水平面上,导轨由两种材料组成.PG右侧部分单位长度电阻为r0,且PQ=QH=GH=L.PG左侧导轨电阻不计,导体棒AC的电阻为R0,整个导轨处于匀强磁场中,磁场方向垂直于导轨平面向下,磁感应强度大小为B.质量为m的导体棒AC在恒力F作用下从静止开始运动,在到达PG之前导体棒AC已经匀速.