��Ŀ����
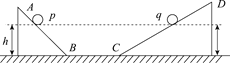
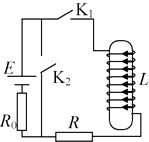
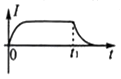
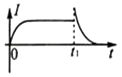
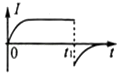
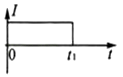
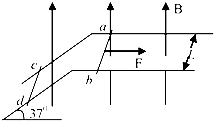
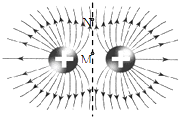
����Ŀ����ͼ��a����ʾ��ƽ�н�����A��B��ľ���Ϊd������A��B���ϼ�����ͼ��b����ʾ�ķ����ε�ѹ��t=0ʱA���B��ĵ��Ƹߣ���ѹ������ֵΪU0 �� ����ֵҲΪU0 �� ����������Ϊm�Ĵ������ҵ����Ϊq��������ɵ�����������AB���е�O��ƽ���ڽ����巽��OO'���ٶ�v0= ![]() �������룬�������Ӳ���ײ������������AB��ķ���ʱ���ΪT����������Ӱ�죮����
�������룬�������Ӳ���ײ������������AB��ķ���ʱ���ΪT����������Ӱ�죮����
��1����������糡ʱ���ٶȴ�С������
��2�����Ӵ���糡ʱλ����O'��ľ��뷶Χ��
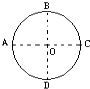
��3����Ҫʹ����糡�����Ӿ�ijһ��ֱֽ���Բ��������ǿ�ų�ƫת���ܵ���Բ�δų��߽��ͬһ���㣬���������ռ�����ų��������С�뾶����Ӧ�ĴŸ�ǿ���Ƕ��
���𰸡�
��1���⣺�ɳ����ӵ��ٶȶ���ͬ�����ص糡�߷����ٶȴ�С��Ϊ ![]() ��
��
�ɳ��ٶȴ�СΪ ![]() =
= ![]() =
= ![]() ��
��
���ٶ�v�ķ����� ![]() �ļн�Ϊ�ȣ���
�ļн�Ϊ�ȣ��� ![]() ��
��
���ԣ�����ˮƽ�������½�Ϊ��=45�㣬��С ![]()
����������糡ʱ���ٶȴ�СΪ ![]() ������ˮƽ�������½�Ϊ��=45�㣻
������ˮƽ�������½�Ϊ��=45�㣻
��2���⣺��������t=nTʱ�̽���糡�����²�������� ![]() ��
��
�� ![]() ��
��
��� ![]()
�������� ![]() ʱ�̽���糡�����ϲ������
ʱ�̽���糡�����ϲ������
�� ![]() ��
��
��� ![]()
���ԣ��ھ���O���е��Ϸ� ![]() ���·�
���·� ![]() ��Χ�������Ӵ��
��Χ�������Ӵ��
�����Ӵ���糡ʱλ����O'��ľ��뷶Χ���ھ���O���е��Ϸ� ![]() ���·�
���·� ![]() ��Χ�������Ӵ����
��Χ�������Ӵ����
��3���⣺Ҫʹƽ�������ܹ�����Բ�δų�����߽�������С����ʱ���ų�ֱ����Сֵ�����ӿ�����ȣ�

���ӿ��� ![]() =
= ![]() ��
��
�ʴų��������С�뾶Ϊ ![]() ��
��
�����ڴų�����Բ���˶��� ![]() ��
��
��� ![]()
����Ҫʹ����糡�����Ӿ�ijһ��ֱֽ���Բ��������ǿ�ų�ƫת���ܵ���Բ�δų��߽��ͬһ���㣬���������ռ�����ų��������С�뾶 ![]() ����Ӧ�ĴŸ�ǿ����
����Ӧ�ĴŸ�ǿ���� ![]()
����������1�������ٶȵĺϳɺͷֽ⽫���ӵ��˶�����ƽ���ڳ��ٶȷ���ʹ�ֱ�ڳ��ٶȵķ��������ֽ⣬��ƽ���ڳ��ٶȷ�������������ֱ���˶����ڴ�ֱ�ڳ��ٶȷ��������ڵ糡����������������ֱ���˶���������������ϵķ��ٶȣ����õ����ٶȼ��ɣ�
��2��������t=0��T��2T��ʱ�̽���ʱ��O��λ��ƫ�����¶ˣ�������t=nT+![]() Tʱʱ�̽���ʱ��O��λ��ƫ�����϶ˣ������˶�ѧ��ʽ��ʽ��⼴�ɣ�
Tʱʱ�̽���ʱ��O��λ��ƫ�����϶ˣ������˶�ѧ��ʽ��ʽ��⼴�ɣ�
��3�������ڴ�����ӵ��ٶȶ�����ͬ�ģ����ٶȺϳɷ�������ӵ��ٶȣ�Ҫʹƽ�������ܹ�����Բ�δų�����߽�������С����ʱ���ų�ֱ����Сֵ�����ӿ�����ȣ����ɵõ��ų��������С�뾶�����ӽ�����ǿ�ų��У������������ṩ����������ţ�ٵڶ����������Ӧ�ĴŸ�ǿ��