题目内容
 如图所示,在竖直平面内固定着一个光滑的四分之一圆狐槽,其上端距地面的高为H,下端的切线方向水平.一个小球从上端由静止开始滑下,则当小球落到地面时的水平距离有最大值时,圆弧槽的半径R为
如图所示,在竖直平面内固定着一个光滑的四分之一圆狐槽,其上端距地面的高为H,下端的切线方向水平.一个小球从上端由静止开始滑下,则当小球落到地面时的水平距离有最大值时,圆弧槽的半径R为| H |
| 2 |
| H |
| 2 |
分析:小球从B点抛出后做平抛运动,根据平抛运动的位移公式列方程,然后利用数学知识分析水平位移的表达式即可求解水平位移的最大值圆弧槽的半径R大小.
解答:解:根据机械能守恒可知,小球平抛的初速度为:
mgR=
mv2,即v=
小球离开B点后做平抛运动,下落高度为H-R,由平抛运动的规律得:
H-R=
gt2,s=vt
解以上方程得:s=
,由上式可知,当R=
时,小球落到地面时的水平距离有最大值.
故答案为:
.
mgR=
| 1 |
| 2 |
| 2gR |
小球离开B点后做平抛运动,下落高度为H-R,由平抛运动的规律得:
H-R=
| 1 |
| 2 |
解以上方程得:s=
| H2-(2R-H)2 |
| H |
| 2 |
故答案为:
| H |
| 2 |
点评:本题关键对两个的运动过程分析清楚,根据平抛运动规律结合数学知识列式求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 (2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( )
(2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( ) 如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( )
如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( ) 如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计)
如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计)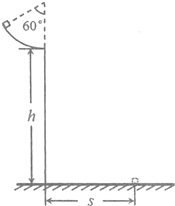 如图所示,在竖直平面内有一个粗糙的
如图所示,在竖直平面内有一个粗糙的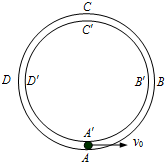 如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.
如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.