题目内容
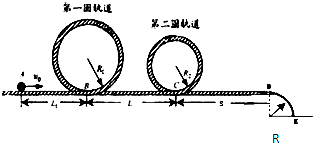 过山车是游乐场中常见的设施.某校物理兴趣小组自制过山车的简易模型,如图所示,它由水平轨道和在竖直平面内的圆形轨道组成,B、C分别是二个圆形轨道的最低点,半径分别是R1=2.0m、R2=1.4M,DE段是一半径为R3=1.0m的四分之一光滑圆弧轨道,它与水平轨道平滑连接,D点为圆弧的最高点,一个质量为M=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动,A、B间距L1=6.0m.C、D间距S=15.0m,小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,试求:
过山车是游乐场中常见的设施.某校物理兴趣小组自制过山车的简易模型,如图所示,它由水平轨道和在竖直平面内的圆形轨道组成,B、C分别是二个圆形轨道的最低点,半径分别是R1=2.0m、R2=1.4M,DE段是一半径为R3=1.0m的四分之一光滑圆弧轨道,它与水平轨道平滑连接,D点为圆弧的最高点,一个质量为M=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动,A、B间距L1=6.0m.C、D间距S=15.0m,小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,试求:(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小;
(2)如果小球恰能通过第二圆形轨道,B、C间距L应是多少;
(3)如果小球从第二圆形轨道运动到水平轨道的D点时,能否沿DE圆弧轨道滑下?若不能请说明理由.
分析:对小球的运动过程进行分析.运用动能定理求出小球经过第一个圆轨道的最高点时的速度,再对小球在第一个圆轨道的最高点进行受力分析,并利用牛顿第二定律求出轨道对小球作用力.知道小球恰能通过圆形轨道的含义,并能找出在第二圆形轨道的最高点速度.运用动能定理研究某一运动过程求出B、C间距L.
解答:解:(1)设小球经过第一个圆轨道的最高点时的速度为v1根据动能定理得:
-μmgL1-2mgR1=
mv12-
mv02 …①
小球在最高点受到重力mg和轨道对它的作用力F,根据牛顿第二定律有:
F+mg=m
… ②
由 ①、②得:F=10.0 N… ③
(2)设小球在第二个圆轨道的最高点的速度为v2,由小球恰能通过第二圆形轨道有:
mg=m
…④
-μmg(L1+L)-2mgR2=
mv22-
mv02…⑤
由④、⑤得:L=12.5m…⑥
(3)不能,
设小球运动到D点时速度为vD根据动能定理可得:
-μmg(L1+L+S)=
mvD2-
mv02 ①
可得vD2=10,在D点恰好通过
mg=
则物体对水平面D点无压力N=0,由此物体只受重力作用,以VD水平速度平抛.
答:(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小是10.0 N;
(2)如果小球恰能通过第二圆形轨道,B、C间距L应是12.5m
(3)如果小球从第二圆形轨道运动到水平轨道的D点时,不能沿DE圆弧轨道滑.
-μmgL1-2mgR1=
| 1 |
| 2 |
| 1 |
| 2 |
小球在最高点受到重力mg和轨道对它的作用力F,根据牛顿第二定律有:
F+mg=m
| ||
| R1 |
由 ①、②得:F=10.0 N… ③
(2)设小球在第二个圆轨道的最高点的速度为v2,由小球恰能通过第二圆形轨道有:
mg=m
| ||
| R2 |
-μmg(L1+L)-2mgR2=
| 1 |
| 2 |
| 1 |
| 2 |
由④、⑤得:L=12.5m…⑥
(3)不能,
设小球运动到D点时速度为vD根据动能定理可得:
-μmg(L1+L+S)=
| 1 |
| 2 |
| 1 |
| 2 |
可得vD2=10,在D点恰好通过
mg=
| ||
| R3 |
则物体对水平面D点无压力N=0,由此物体只受重力作用,以VD水平速度平抛.
答:(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小是10.0 N;
(2)如果小球恰能通过第二圆形轨道,B、C间距L应是12.5m
(3)如果小球从第二圆形轨道运动到水平轨道的D点时,不能沿DE圆弧轨道滑.
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.知道小球恰能通过圆形轨道的含义以及要使小球不能脱离轨道的含义.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目

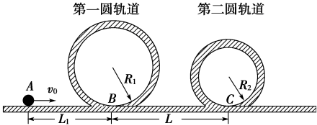 是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以
是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以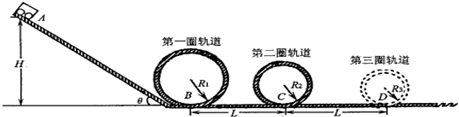
 过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求: 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求: