题目内容
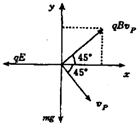
(1)小物体A下落至N点时开始离开墙壁,说明这时小物体A与墙壁之间已无挤压,弹力为零.
故有:qE=qvNB
∴vN=
| E |
| B |
| 4 |
| 2 |
对小物体A从M点到N点的过程应用动能定理,这一过程电场力和洛仑兹力均不做功,应有:
mgh-Wf克=
| 1 |
| 2 |
| v | 2N |
∴Wf克=mgh-
| 1 |
| 2 |
| v | 2N |
| 1 |
| 2 |
(2)小物体离开N点做曲线运动到达P点时,受力情况如图所示,由于θ=45°,物体处于平衡状态,建立如图的坐标系,可列出平衡方程.
qBvpcos45°-qE=0 (1)
qBvpsin45°-mg=0 (2)
由(1)得 vp=
| E |
| Bcos45° |
| 2 |
由(2)得 q=
| mg |
| Bvpsin45° |
N→P过程,由动能定理得mg(H-h)-qES=
| 1 |
| 2 |
| v | 2p |
| 1 |
| 2 |
| v | 21 |
代入计算得 S=0.6 m
答:(1)A沿壁下滑时克服摩擦力做的功6×l0-3 J.
(2)P与M的水平距离s是0.6m.

(1)小物体A下落至N点时开始离开墙壁,说明这时小物体A与墙壁之间已无挤压,弹力为零.
故有:qE=qvNB
∴vN=
| E |
| B |
| 4 |
| 2 |
对小物体A从M点到N点的过程应用动能定理,这一过程电场力和洛仑兹力均不做功,应有:
mgh-Wf克=
| 1 |
| 2 |
| v | 2N |
∴Wf克=mgh-
| 1 |
| 2 |
| v | 2N |
| 1 |
| 2 |
(2)小物体离开N点做曲线运动到达P点时,受力情况如图所示,由于θ=45°,物体处于平衡状态,建立如图的坐标系,可列出平衡方程.
qBvpcos45°-qE=0 (1)
qBvpsin45°-mg=0 (2)
由(1)得 vp=
| E |
| Bcos45° |
| 2 |
由(2)得 q=
| mg |
| Bvpsin45° |
N→P过程,由动能定理得mg(H-h)-qES=
| 1 |
| 2 |
| v | 2p |
| 1 |
| 2 |
| v | 21 |
代入计算得 S=0.6 m
答:(1)A沿壁下滑时克服摩擦力做的功6×l0-3 J.
(2)P与M的水平距离s是0.6m.

练习册系列答案
相关题目
 (2011?苏州二模)为探究物体在下落过程中机械能是否守恒,某同学采用实验装置如图甲所示.
(2011?苏州二模)为探究物体在下落过程中机械能是否守恒,某同学采用实验装置如图甲所示.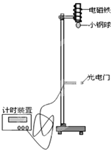 (Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.
(Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.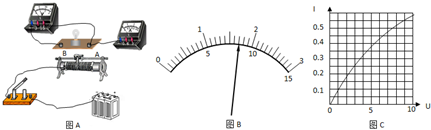

 );
); )数据;
)数据; 坐标系中找到对应的坐标点,拟合得到如图乙所示直线.
坐标系中找到对应的坐标点,拟合得到如图乙所示直线.