题目内容
正方形闭合线圈置于匀强磁场中,线框平面与磁场方向垂直,线圈电阻不能忽略.用力将线框分别以速度v1、v2匀速拉出磁场,且v1>v2,在这两个过程中,通过导线横截面的电荷量q1:q2= ,线框中产生的焦耳热Q1:Q2= ,线框所受安培力大小F1:F2= .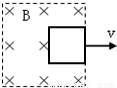
【答案】分析:根据法拉第电磁感应定律、欧姆定律推导出电荷量的表达式,再电荷量之比.根据焦耳定律研究热量之比.由公式F=BIL研究安培力之比.
解答:解:由法拉第电磁感应定律得
感应电动势 E=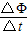
由欧姆定律得I=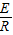
则通过导线的电荷量为q=I△t
得到q=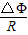 ,与线框移动速度无关,磁通量的变化量△Φ相同,所以通过导线横截面的电荷量q1:q2=1:1.
,与线框移动速度无关,磁通量的变化量△Φ相同,所以通过导线横截面的电荷量q1:q2=1:1.
根据焦耳定律得
焦耳热Q=I2Rt=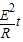 =
=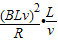 =
=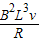 ,所以线框中产生的焦耳热Q1:Q2=v1:v2.
,所以线框中产生的焦耳热Q1:Q2=v1:v2.
安培力F=BIL=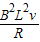 ,所以线框所受安培力大小F1:F2=v1:v2.
,所以线框所受安培力大小F1:F2=v1:v2.
故答案为:1:1,v1:v2.v1:v2.
点评:本题采用比例法,用相同的物理量表示所求量,再求比例,是常用的方法.常见问题.
解答:解:由法拉第电磁感应定律得
感应电动势 E=
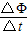
由欧姆定律得I=
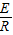
则通过导线的电荷量为q=I△t
得到q=
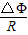 ,与线框移动速度无关,磁通量的变化量△Φ相同,所以通过导线横截面的电荷量q1:q2=1:1.
,与线框移动速度无关,磁通量的变化量△Φ相同,所以通过导线横截面的电荷量q1:q2=1:1.根据焦耳定律得
焦耳热Q=I2Rt=
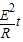 =
=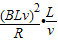 =
=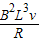 ,所以线框中产生的焦耳热Q1:Q2=v1:v2.
,所以线框中产生的焦耳热Q1:Q2=v1:v2.安培力F=BIL=
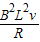 ,所以线框所受安培力大小F1:F2=v1:v2.
,所以线框所受安培力大小F1:F2=v1:v2. 故答案为:1:1,v1:v2.v1:v2.
点评:本题采用比例法,用相同的物理量表示所求量,再求比例,是常用的方法.常见问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 正方形闭合线圈置于匀强磁场中,线框平面与磁场方向垂直,线圈电阻不能忽略.用力将线框分别以速度v1、v2匀速拉出磁场,且v1>v2,在这两个过程中,通过导线横截面的电荷量q1:q2=
正方形闭合线圈置于匀强磁场中,线框平面与磁场方向垂直,线圈电阻不能忽略.用力将线框分别以速度v1、v2匀速拉出磁场,且v1>v2,在这两个过程中,通过导线横截面的电荷量q1:q2= 、
、 匀速拉出磁场,且
匀速拉出磁场,且 ,在这两个过程中,通过导线横截面的电荷量
,在这两个过程中,通过导线横截面的电荷量 = ,线框中产生的焦耳热
= ,线框中产生的焦耳热 = ,线框所受安培力大小
= ,线框所受安培力大小 。
。
 、
、 匀速拉出磁场,且
匀速拉出磁场,且 ,在这两个过程中,通过导线横截面的电荷量
,在这两个过程中,通过导线横截面的电荷量 = ,线框中产生的焦耳热
= ,线框中产生的焦耳热 = ,线框所受安培力大小
= ,线框所受安培力大小 。
。
