��Ŀ����
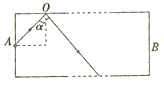
13�� ��ͼ��ʾ������ΪM�����Ϊ�ȵ�б����A����ˮƽ�����ϣ�������Ϊm��С����B����б����A�Ķ��ˣ����˵ĸ߶�Ϊh����ʼʱ���߱�����Ծ�ֹ��Ȼ��B��A�Ķ�������б�滬�����森���Ե���Ϊ�ο�ϵ���Һ���һ��Ħ�������ڴ˹����У�б���֧������B�����Ĺ�ΪW�����������W���ĸ�����ʽ�У�ֻ��һ���Ǻ����ģ�����ܲ�����⣬���������ͨ�������������б���ʽ�����������жϣ���������жϣ�W�ĺ�������ʽӦΪ��������
��ͼ��ʾ������ΪM�����Ϊ�ȵ�б����A����ˮƽ�����ϣ�������Ϊm��С����B����б����A�Ķ��ˣ����˵ĸ߶�Ϊh����ʼʱ���߱�����Ծ�ֹ��Ȼ��B��A�Ķ�������б�滬�����森���Ե���Ϊ�ο�ϵ���Һ���һ��Ħ�������ڴ˹����У�б���֧������B�����Ĺ�ΪW�����������W���ĸ�����ʽ�У�ֻ��һ���Ǻ����ģ�����ܲ�����⣬���������ͨ�������������б���ʽ�����������жϣ���������жϣ�W�ĺ�������ʽӦΪ��������| A�� | W=0 | B�� | W=-$\frac{{Mmh{{sin}^2}��}}{{��{M+m}����{M+m{{sin}^2}��}��}}$g | ||
| C�� | W=$\frac{{Mmh{{cos}^2}��}}{{��{M+m}����{M+m{{sin}^2}��}��}}$g | D�� | W=-$\frac{M{m}^{2}h{cos}^{2}��}{��M+m����M+m{sin}^{2}�ȣ�}g$ |
���� ����б�����ڹ⻬��ˮƽ���ϣ���û�й̶���������б������û�ʹб����ˣ�����б����ˣ���������б���»�·�������нǣ��ȣ����������Ź̶�б���»���Ȼ��ͬ�����ں���һ��Ħ���������ڴ�ʱб���֧������B��λ�Ʒ���ɶ۽ǣ�����б���֧������B����������
��� �⣺A������б�����ڹ⻬��ˮƽ���ϣ���û�й̶���������б������û�ʹб����ˣ�����б����ˣ���������б���»�·�������нǣ��ȣ����������Ź̶�б���»���Ȼ��ͬ������ϵͳ��Ħ�������ڴ�ʱб���֧������B��λ�Ʒ���ɶ۽ǣ�����б���֧������B������������A����C����
B�����ĵ�λΪ1J=1N•m��
���յ�λ�ƣ�$\frac{M{m}^{2}h{cos}^{2}��}{��M+m����M+m{sin}^{2}�ȣ�}g$�ĵ�λ��N•m��$\frac{Mmh{sin}^{2}��}{��M+m����M+m{sin}^{2}�ȣ�}$�ĵ�λ��m����B����D��ȷ��
��ѡ��D��
���� ���⿼���˵�λ�ƺ����������жϣ����������Ŀ��Ҫ������������ѧ��֪ʶ����̭�����д�����

��ϰ��ϵ�д�
�����Ŀ
4�� ��ͼ��ʾ��A��BΪ������������������������ǣ����з�����ͬ��A��B���ǵĹ���뾶�ֱ�Ϊra��b��ijʱ��A��B�����Ǿ��뵽���������֪����A����������ΪT���Ӹ�ʱ����A��B�������Զ�����������ʱ��Ϊ��������
��ͼ��ʾ��A��BΪ������������������������ǣ����з�����ͬ��A��B���ǵĹ���뾶�ֱ�Ϊra��b��ijʱ��A��B�����Ǿ��뵽���������֪����A����������ΪT���Ӹ�ʱ����A��B�������Զ�����������ʱ��Ϊ��������
 ��ͼ��ʾ��A��BΪ������������������������ǣ����з�����ͬ��A��B���ǵĹ���뾶�ֱ�Ϊra��b��ijʱ��A��B�����Ǿ��뵽���������֪����A����������ΪT���Ӹ�ʱ����A��B�������Զ�����������ʱ��Ϊ��������
��ͼ��ʾ��A��BΪ������������������������ǣ����з�����ͬ��A��B���ǵĹ���뾶�ֱ�Ϊra��b��ijʱ��A��B�����Ǿ��뵽���������֪����A����������ΪT���Ӹ�ʱ����A��B�������Զ�����������ʱ��Ϊ��������| A�� | $\frac{T}{2��\sqrt{��\frac{{r}_{a}}{{r}_{b}}��^{3}}+1��}$ | B�� | $\frac{T}{\sqrt{��\frac{{r}_{a}}{{r}_{b}}��^{3}}-1}$ | C�� | $\frac{T}{2��\sqrt{��\frac{{r}_{a}}{{r}_{b}}��^{3}}-1��}$ | D�� | $\frac{T}{\sqrt{��\frac{{r}_{a}}{{r}_{b}}��^{3}}+1}$ |
18������ΪR�ĸ��ؽӵ�20Vֱ����ѹ�����ĵĵ繦����P��һ����ѹ����ԭ��Ȧ�����ֵΪ200V�����ҽ�����ѹ������Ȧ�ӵ���RҪʹR�����ĵĵ繦��Ϊ$\frac{P}{2}$�����ѹ��ԭ������Ȧ������֮��Ϊ��������
| A�� | 20��1 | B�� | 10$\sqrt{2}$��1 | C�� | 10��1 | D�� | 1��10 |
3�� ��ͼ��ʾ���ס�������������ͬ�����������ֵ�ɵĴ������ӣ��Բ�ͬ�����ʾ�С��P��ֱ�ų��߽�MN�����뷽��ֱֽ���������ǿ�ų��У��ڴų���������Բ���˶�������ֱ�ų��߽�MN����ų�����Բ�켣��ͼ��������ʾ������������������������������������˵������ȷ���ǣ�������
��ͼ��ʾ���ס�������������ͬ�����������ֵ�ɵĴ������ӣ��Բ�ͬ�����ʾ�С��P��ֱ�ų��߽�MN�����뷽��ֱֽ���������ǿ�ų��У��ڴų���������Բ���˶�������ֱ�ų��߽�MN����ų�����Բ�켣��ͼ��������ʾ������������������������������������˵������ȷ���ǣ�������
 ��ͼ��ʾ���ס�������������ͬ�����������ֵ�ɵĴ������ӣ��Բ�ͬ�����ʾ�С��P��ֱ�ų��߽�MN�����뷽��ֱֽ���������ǿ�ų��У��ڴų���������Բ���˶�������ֱ�ų��߽�MN����ų�����Բ�켣��ͼ��������ʾ������������������������������������˵������ȷ���ǣ�������
��ͼ��ʾ���ס�������������ͬ�����������ֵ�ɵĴ������ӣ��Բ�ͬ�����ʾ�С��P��ֱ�ų��߽�MN�����뷽��ֱֽ���������ǿ�ų��У��ڴų���������Բ���˶�������ֱ�ų��߽�MN����ų�����Բ�켣��ͼ��������ʾ������������������������������������˵������ȷ���ǣ�������| A�� | �״�����ɣ��Ҵ������ | |
| B�� | ���������Լ������� | |
| C�� | �����ʴ����ҵ����� | |
| D�� | ���ڴų����˶���ʱ��������ڴų����˶���ʱ�� |


 ��ͼ��ʾ��ABΪһֱ���ά��AB֮�����Ϊs��ʹһ�������źŴӹ��ά�м����䣬������ڹ��ά������Ľ�����ǡ�÷���ȫ���䣬��A�㴫�䵽B������ʱ��Ϊt������ά���ò��ϵ�������n��
��ͼ��ʾ��ABΪһֱ���ά��AB֮�����Ϊs��ʹһ�������źŴӹ��ά�м����䣬������ڹ��ά������Ľ�����ǡ�÷���ȫ���䣬��A�㴫�䵽B������ʱ��Ϊt������ά���ò��ϵ�������n��