题目内容

如右图所示，轻杆的一端固定一光滑球体，杆的另一端O为自由转动轴，而球又搁置在光滑斜面上．若杆与墙面的夹角为β，斜面倾角为θ，开始时轻杆与竖直方向的夹角β<θ.且θ＋β<90°，则为使斜面能在光滑水平面上向右做匀速直线运动，在球体离开斜面之前，作用于斜面上的水平外力F的大小及轻杆受力FT和地面对斜面的支持力FN的大小变化情况是(　　)

A．F逐渐增大，FT逐渐减小，FN逐渐减小

B．F逐渐减小，FT逐渐减小，FN逐渐增大

C．F逐渐增大，FT先减小后增大，FN逐渐增大

D．F逐渐减小，FT先减小后增大，FN逐渐减小

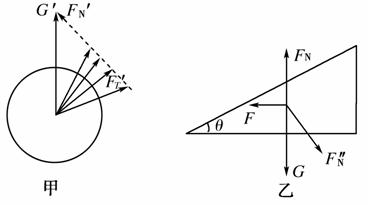
解析：　利用矢量三角形法对球体进行分析如图甲所示，可知F′T是先减小后增大，根据牛顿第三定律，FT先减小后增大．斜面对球的支持力F′N逐渐增大．对斜面受力分析如图乙所示，可知F＝F″Nsin θ；因为F″N＝F′N(作用力反作用力)，F′N逐渐增大，所以F″N逐渐增大，F逐渐增大，水平面对斜面的支持力FN＝G＋F″N·cos θ，故FN逐渐增大．