题目内容
 用长为L的绝缘细线拴一个质量为m,电荷量为q的小球,如图所示,线的另一端固定在水平方向的匀强电场中,开始时将带电球拉到使线成水平的位置,小球由静止从A点向下摆动,当细线转过60°角,小球到达B点时,速度恰好为零,试求:
用长为L的绝缘细线拴一个质量为m,电荷量为q的小球,如图所示,线的另一端固定在水平方向的匀强电场中,开始时将带电球拉到使线成水平的位置,小球由静止从A点向下摆动,当细线转过60°角,小球到达B点时,速度恰好为零,试求:(1)匀强电场的场强E为多大?
(2)小球由A运动到B点的过程中,细线的最大拉力多大?
(3)在A点给小球一竖直向下的初速度使小球能完成竖直平面内的完整的圆周运动,求小球速度最小的点的电势.(设O点的电势为零,电场区域足够大,小球始终在匀强电场中)
分析:(1)根据动能定理即可求解电场强度.
(2)找到小球运动的最低点,也就是速度最大的点,此时绳子的拉力最大,根据动能定理及向心力公式即可求解.
(3)小球恰好由电场力与重力的合力提供向心力时,小球通过此位置就能做完整的圆周运动,根据U=ELsinα求解.
(2)找到小球运动的最低点,也就是速度最大的点,此时绳子的拉力最大,根据动能定理及向心力公式即可求解.
(3)小球恰好由电场力与重力的合力提供向心力时,小球通过此位置就能做完整的圆周运动,根据U=ELsinα求解.
解答:解:(1)小球从A到B的运动过程中运用动能定理的:
-EqL(1-cos60°)+mgLsin60°=0
解得:E=
(2)当小球运动到细线方向与电场力和重力合力的方向相反时,绳子的拉力最大,
设此时绳子与水平方向夹角为θ,则tanθ=
=
所以θ=30°
根据动能定理得:
mgLsinθ-Eq(1-cosθ)L=
mv2
T-F合=m
F合=
由上述各式解得:T=(6-2
)mg
(3)小球速度最小的点应在与C位置在同一直径上的C′点,如图所示

则有:U=ELsin60°
解得:φ=
答:(1)匀强电场的场强E为
;
(2)小球由A运动到B点的过程中,细线的最大拉力为(6-2
)mg;
(3)小球速度最小的点的电势为
-EqL(1-cos60°)+mgLsin60°=0
解得:E=
| ||
| q |
(2)当小球运动到细线方向与电场力和重力合力的方向相反时,绳子的拉力最大,
设此时绳子与水平方向夹角为θ,则tanθ=
| mg |
| Eq |
| ||
| 3 |
所以θ=30°
根据动能定理得:
mgLsinθ-Eq(1-cosθ)L=
| 1 |
| 2 |
T-F合=m
| v2 |
| L |
F合=
| mg2+(Eq)2 |
由上述各式解得:T=(6-2
| 3 |
(3)小球速度最小的点应在与C位置在同一直径上的C′点,如图所示

则有:U=ELsin60°
解得:φ=
| 3mgL |
| 2q |
答:(1)匀强电场的场强E为
| ||
| q |
(2)小球由A运动到B点的过程中,细线的最大拉力为(6-2
| 3 |
(3)小球速度最小的点的电势为
| 3mgL |
| 2q |
点评:本题是动能定理和牛顿第二定律的综合应用,难点是找到等效的最高点,此位置小球由电场力与重力的合力提供向心力.

练习册系列答案
相关题目
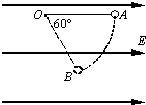 如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场E中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求:
如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场E中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求: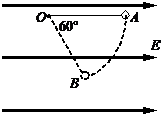 如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场E中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求:
如图所示,用长为l的绝缘细线拴一个质量为m、带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀强电场E中.将小球拉至使悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过60°角到达位置B时,速度恰好为零.求: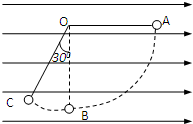 如图所示,用长为l的绝缘细线拴一个质量为m.带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀速电场E中.将小球拉至悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过与竖直方向成300角到达位置C时,速度恰好为零.求:
如图所示,用长为l的绝缘细线拴一个质量为m.带电量为+q的小球(可视为质点)后悬挂于O点,整个装置处于水平向右的匀速电场E中.将小球拉至悬线呈水平的位置A后,由静止开始将小球释放,小球从A点开始向下摆动,当悬线转过与竖直方向成300角到达位置C时,速度恰好为零.求: