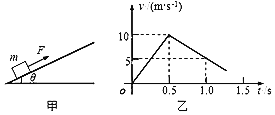��Ŀ����
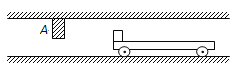
����Ŀ����ͼ��ʾ�����Ϊ30o�Ĺ⻬б��AB��L1=0.4m��B�˾�ˮƽ����h=0.8m��O��B������·���B���Ҷ˽�һ�⻬СԲ����ͼ��δ��������Բ���Ҷ�����ˮƽ������һ��L2=1.0m��ˮƽľ��MNƽ�����ӣ�С�����A���ɾ�ֹ�ͷź��˶���N��ǡ��ֹͣ��
��1���鵽��B���ٶ�vB�Ĵ�С��
��2������ľ��MN֮��Ķ�Ħ�������̣�
��3������ľ���Ҳ��ȥ��Ϊ��L��һ�Σ������A���ɾ�ֹ�ͷź���ľ�壬����ˮƽ������ij��P��ͼ��δ�����������ص�P��O��ľ��뷶Χ��
���𰸡�
��1���⣺������б�������ȼ����˶������ݻ�е���غ㶨�ɵã�
mgL1sin30��= ![]()
�������ݽ�ã�vB=2m/s
�𣺻��鵽��B���ٶ�vB�Ĵ�С��2m/s��
��2���⣺������ˮƽ�������ȼ����˶��������M�˶���N���������ܵ�Ħ������СΪ��f=��N=��mg
���ݶ��ܶ����ã���fL2=0�� ![]()
�������ݽ�ã���=0.2
�𣺻�����ľ��MN֮��Ķ�Ħ����������0.2��
��3���⣺

�ⷨһ��
��ľ���Ҳ��ȡ����Ϊ��L�����뿪ľ�����ƽ���˶�����ƽ�ij��ٶ�Ϊv0����
![]() =��2a2��L2����L��
=��2a2��L2����L��
�� v0= ![]()
�� h= ![]() ��x=v0t=
��x=v0t= ![]()
�������ݵã�x=0.8 ![]()
��ص�P��O��ľ��� S=L2����L+x=L2����L+0.8 ![]()
![]() ��ȡֵ��ΧΪ��0��1]����������ͼ�����κ�����ֵ���ɵ�
��ȡֵ��ΧΪ��0��1]����������ͼ�����κ�����ֵ���ɵ�
�� ![]() =0.4ʱ������L=0.16mʱ��S�����ֵΪ��Smax=1.16m
=0.4ʱ������L=0.16mʱ��S�����ֵΪ��Smax=1.16m
�� ![]() =1ʱ������L=1mʱ��S����СֵΪ��Smin=0.8m
=1ʱ������L=1mʱ��S����СֵΪ��Smin=0.8m
���� 0.8m��S��1.16m
�ⷨ������ľ���Ҳ��ȡ����Ϊ��L�����뿪ľ�����ƽ���˶�����ƽ�ij��ٶ�Ϊv0��������˼ά���У�
![]() =2��g��L
=2��g��L
����ƽ���˶����У�
S=L2����L+v0t=L2����L+0.8 ![]()
![]() ��ȡֵ��ΧΪ��0��1]����������ͼ�����κ�����ֵ���ɵ�
��ȡֵ��ΧΪ��0��1]����������ͼ�����κ�����ֵ���ɵ�
�� ![]() =0.4ʱ������L=0.16mʱ��S�����ֵΪ��Smax=1.16m
=0.4ʱ������L=0.16mʱ��S�����ֵΪ��Smax=1.16m
�� ![]() =1ʱ������L=1mʱ��S����СֵΪ��Smin=0.8m
=1ʱ������L=1mʱ��S����СֵΪ��Smin=0.8m
��ã�0.8m��S��1.16m
����ص�P��O��ľ��뷶ΧΪ0.8m��S��1.16m��
��������������б�������ȼ����˶������ݻ�е���غ㶨�ɵó�B���ٶȣ�������ˮƽ�������ȼ����˶��������M�˶���N���������ö��ܶ������������Ħ��������ƽ���˶�֪ʶ�ó�����ˮƽ������ij��P������L�Ĺ�ϵ��
�����㾫����������Ҫ�������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ��ƽ���˶������֪ʶ�㣬��Ҫ�����ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ���ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶�������ȷ�����⣮

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�