题目内容
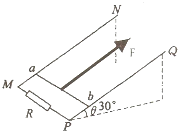 (2008?湛江二模)如图所示,足够长的光滑平行导轨MN、PQ倾斜放置,两导轨间的距离为L=1.0m,导轨平面与水平面间的夹角为30°,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为R=3.5Ω的电阻,金属棒ab垂直于导轨放置,金属棒ab的质量m=0.20kg,电阻r=0.50Ω,并与导轨保持良好接触.现在ab上作用一恒力F=5.0N,方向垂直于ab并沿导轨平面向上,使金属棒ab由静止开始运动,在M处安装一个距离传感器(图中未画出),可以测出金属棒ab在运动中离MP的距离与时间的该关系,如下表所示.不计导轨的电阻,取g=10m/s2.求:
(2008?湛江二模)如图所示,足够长的光滑平行导轨MN、PQ倾斜放置,两导轨间的距离为L=1.0m,导轨平面与水平面间的夹角为30°,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为R=3.5Ω的电阻,金属棒ab垂直于导轨放置,金属棒ab的质量m=0.20kg,电阻r=0.50Ω,并与导轨保持良好接触.现在ab上作用一恒力F=5.0N,方向垂直于ab并沿导轨平面向上,使金属棒ab由静止开始运动,在M处安装一个距离传感器(图中未画出),可以测出金属棒ab在运动中离MP的距离与时间的该关系,如下表所示.不计导轨的电阻,取g=10m/s2.求:| 时间t/s | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| 棒离MP的距离s/m | 0.01 | 0.06 | 0.18 | 0.36 | 0.61 | 1.01 | 1.41 |
(2)电阻R在0.6s内产生的热量为多少?
分析:(1)分析表格数据,研究ab棒的运动情况.从表格数据看出,ab棒最终做匀速直线运动,根据公式v=
求出匀速直线运动的速度.此时棒所受的合力为零.由E=BLv、I=
、F=BIL推导出安培力表达式,根据平衡条件列式,即可求解B;
(2)由表格读出在0.6s内棒的位移s=1.41m-0.01m=1.4m,根据功能关系:外力做功等于棒的动能增加量、焦耳热和重力势能增加量三者之和,根据能量守恒列式,求出电路中产生的热量Q,电阻R在0.6s内产生的热量QR=
Q
| △s |
| △t |
| E |
| R+r |
(2)由表格读出在0.6s内棒的位移s=1.41m-0.01m=1.4m,根据功能关系:外力做功等于棒的动能增加量、焦耳热和重力势能增加量三者之和,根据能量守恒列式,求出电路中产生的热量Q,电阻R在0.6s内产生的热量QR=
| R |
| R+r |
解答:解:(1)由表格数据分析可知,ab棒最终做匀速直线运动,匀速运动的速度为v=
=
=4m/s
金属棒产生的感应电动势为E=E=BLv
回路中感应电流为I=
金属棒受到的安培力为FB=BIL
则得安培力表达式为FB=
根据平衡条件得:F=FB+mgsinθ
联立解得,B=2T
(2)由表格读出:在0.6s内棒的位移s=1.41m-0.01m=1.4m,设回路产生的总热量为Q,由能的转化和守恒定律得
Fs=mgs?sinθ+Q+
mv2
在回路中电阻产生的热量与电阻成正比,则
电阻R在0.6s内产生的热量QR=
Q
联立解得,QR=3.5J
答:(1)所加磁场的磁感应强度B为2T.
(2)电阻R在0.6s内产生的热量为3.5J.
| △s |
| △t |
| 0.4m |
| 0.1s |
金属棒产生的感应电动势为E=E=BLv

回路中感应电流为I=
| E |
| R+r |
金属棒受到的安培力为FB=BIL
则得安培力表达式为FB=
| B2L2v |
| R+r |
根据平衡条件得:F=FB+mgsinθ
联立解得,B=2T
(2)由表格读出:在0.6s内棒的位移s=1.41m-0.01m=1.4m,设回路产生的总热量为Q,由能的转化和守恒定律得
Fs=mgs?sinθ+Q+
| 1 |
| 2 |
在回路中电阻产生的热量与电阻成正比,则
电阻R在0.6s内产生的热量QR=
| R |
| R+r |
联立解得,QR=3.5J
答:(1)所加磁场的磁感应强度B为2T.
(2)电阻R在0.6s内产生的热量为3.5J.
点评:本题是电磁感应中能量问题,要能根据表格中的信息研究棒的运动情况,关键要推导出安培力表达式.此题容易产生的错误是把整个回路产生的热量Q当成金属棒产生的热量.

练习册系列答案
相关题目
 (2008?湛江二模)如图,有一理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端接有一个交流电流表和一个电动机.电动机线圈电阻为R.当输入端接通电源后,电流表读数为I,电动机带动一重物匀速上升.下列判断正确( )
(2008?湛江二模)如图,有一理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端接有一个交流电流表和一个电动机.电动机线圈电阻为R.当输入端接通电源后,电流表读数为I,电动机带动一重物匀速上升.下列判断正确( ) (2008?湛江二模)如图所示电路可将声音信号转化为电信号,该电路中右侧固定不动的金属板 b 与能在声波驱动下沿水平方向振动的镀有金属层的振动膜 a 构成了一个电容器,a、b 通过导线与恒定电源两极相接.若声源 S 做简谐运动,则( )
(2008?湛江二模)如图所示电路可将声音信号转化为电信号,该电路中右侧固定不动的金属板 b 与能在声波驱动下沿水平方向振动的镀有金属层的振动膜 a 构成了一个电容器,a、b 通过导线与恒定电源两极相接.若声源 S 做简谐运动,则( ) (2008?湛江二模)如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高的一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距
(2008?湛江二模)如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高的一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距