题目内容
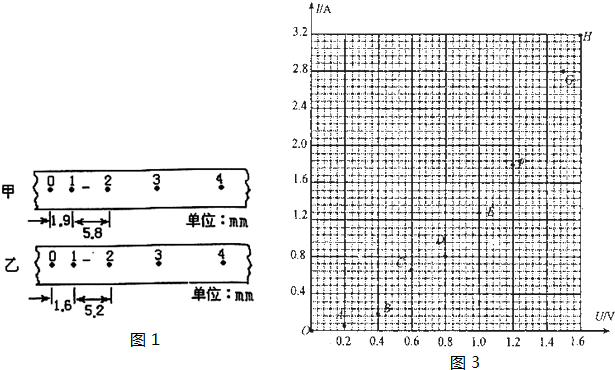
在“验证机械能守恒定律”的实验中,质量m=1.00kg的重物自由下落,带动纸带打出一系列的点,如图所示.相邻计数点间的时间间隔为0.02s;(g=9.8m/s2,计算结果小数点后保留2位有效数字)(1)纸带的 (填“左”或“右”)端与重物相连;
(2)打点计时器打下计数点B时,物体的速度vB= m/s;
(3)从起点O到打下计数点B的过程中物体的动能增加量△EK= J,势能减少量△EP= J;
(4)通过计算发现,数值上△EK △EP(填“>”,“=”或“<”),这是因为在重锤下落过程中存在着阻力的作用.我们可以通过该实验装置测定该阻力的大小,方法如下:先通过纸带测得下落的加速度a= m/s2.再根据牛顿第二定律计算出重锤在下落的过程中受到的平均阻力f= N.

【答案】分析:纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度.从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
该实验的误差主要来源于纸带和打点计时器的摩擦以及空气阻力的存在.
解答:解:(1)与重物相连的纸带一端应该先打出点,先打出点的速度较小,点之间的距离较小,从纸带图上可以看出是左端与重物相连;
(2)利用匀变速直线运动的推论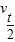 =
=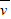
vB=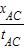 =
=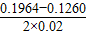 =1.76m/s
=1.76m/s
(3)从起点O到打下计数点B的过程中物体的动能增加量△EK=EkB= mvB2=1.5488J=1.55J.
mvB2=1.5488J=1.55J.
重力势能减小量△Ep=mgh=1×9.8×0.1593J=1.56114J=1.56J.
(4)通过计算发现,数值上△EK<△EP,
物体下落的加速度a=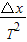 =
=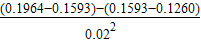 =9.5m/s2,
=9.5m/s2,
根据牛顿第二定律可以得到mg-f=ma,所以f=mg-ma=m(g-a)=1×(9.8-9.5)N=0.3N,
故答案为:(1)左
(2)1.76
(3)1.55,1.56
(4)<;9.5;0.3.
点评:纸带问题的处理时力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
该实验的误差主要来源于纸带和打点计时器的摩擦以及空气阻力的存在.
解答:解:(1)与重物相连的纸带一端应该先打出点,先打出点的速度较小,点之间的距离较小,从纸带图上可以看出是左端与重物相连;
(2)利用匀变速直线运动的推论
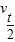 =
=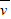
vB=
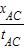 =
=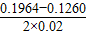 =1.76m/s
=1.76m/s(3)从起点O到打下计数点B的过程中物体的动能增加量△EK=EkB=
 mvB2=1.5488J=1.55J.
mvB2=1.5488J=1.55J.重力势能减小量△Ep=mgh=1×9.8×0.1593J=1.56114J=1.56J.
(4)通过计算发现,数值上△EK<△EP,
物体下落的加速度a=
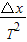 =
=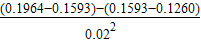 =9.5m/s2,
=9.5m/s2,根据牛顿第二定律可以得到mg-f=ma,所以f=mg-ma=m(g-a)=1×(9.8-9.5)N=0.3N,
故答案为:(1)左
(2)1.76
(3)1.55,1.56
(4)<;9.5;0.3.
点评:纸带问题的处理时力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?成都二模)(1)在验证“机械能守恒定率”的试验中:
(2010?成都二模)(1)在验证“机械能守恒定率”的试验中:
