题目内容
一足够长水平浅色传送带以V0匀速运动，现将一可视为质点的小煤块轻放在其上方，已知煤块与传送带间的动摩擦因数为μ．经过一定时间后达到共同速度．令传送带突然停下，以后不再运动，到最后煤块也停下．已知重力加速度为g．求：
（1）煤块第一次达到与传送带相对静止所用的时间；
（2）煤块在传送带上划出的痕迹长度．
（1）煤块第一次达到与传送带相对静止所用的时间；
（2）煤块在传送带上划出的痕迹长度．
分析：（1）由牛顿第二定律求出煤块的加速度，然后由速度公式求出煤块相对传送带静止所需要的时间．
（2）由匀变速运动规律求出煤块相对于传输带的位移，然后求出痕迹的长度．
（2）由匀变速运动规律求出煤块相对于传输带的位移，然后求出痕迹的长度．
解答：解：（1）以煤块为研究对象，由牛顿第二定律得：μmg=ma，
解得，煤块的加速度a=μg，
达到V0所用时间t=
=
；
（2）在煤块与传送带达到共同速度的过程中，
传送带运动的距离x1=v0t=
煤块运动的距离x2=
at2=
此过程中划出的痕迹长度为△x1=x1-x2=
传送带突然停下后，煤块继续做匀减速运动，直至停下，
这一过程煤块向前运动的距离为x3=
，
考虑重叠部分，最终划出的痕迹长度为x=
；
答：（1）煤块第一次达到与传送带相对静止所用的时间为
；
（2）煤块在传送带上划出的痕迹长度为
．
解得，煤块的加速度a=μg，
达到V0所用时间t=
| v0 |
| a |
| v0 |
| μg |
（2）在煤块与传送带达到共同速度的过程中，
传送带运动的距离x1=v0t=
| ||
| μg |
煤块运动的距离x2=
| 1 |
| 2 |
| ||
| 2μg |
此过程中划出的痕迹长度为△x1=x1-x2=
| ||
| 2μg |
传送带突然停下后，煤块继续做匀减速运动，直至停下，
这一过程煤块向前运动的距离为x3=
| ||
| 2μg |
考虑重叠部分，最终划出的痕迹长度为x=
| ||
| μg |
答：（1）煤块第一次达到与传送带相对静止所用的时间为
| v0 |
| μg |
（2）煤块在传送带上划出的痕迹长度为
| ||
| 2μg |
点评：分析清楚煤块的运动过程，应用牛顿第二定律与运动学公式即可正确解题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
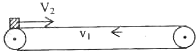如图所示，水平浅色传送带以V1=2m/s的速 度逆时针匀速传送，一质量为m=2kg的煤块以V2=4m/S的初速度从最左端滑上传送带，两者的动摩擦系数μ=0.2，假设皮带足够长且不考虑煤块质量的变化．
如图所示，水平浅色传送带以V1=2m/s的速 度逆时针匀速传送，一质量为m=2kg的煤块以V2=4m/S的初速度从最左端滑上传送带，两者的动摩擦系数μ=0.2，假设皮带足够长且不考虑煤块质量的变化．
