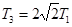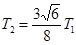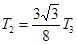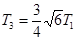题目内容
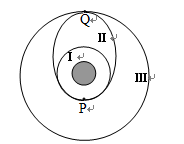
 如图所示,某次发射远地圆轨道卫星时,先让卫星进入一个近地的圆轨道Ⅰ,在此轨道运行的卫星的轨道半径为R1、周期为T1;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为T2;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为R3、周期为T3(轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点).已知R3=2R1,则下列关系正确的是( )
如图所示,某次发射远地圆轨道卫星时,先让卫星进入一个近地的圆轨道Ⅰ,在此轨道运行的卫星的轨道半径为R1、周期为T1;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为T2;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为R3、周期为T3(轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点).已知R3=2R1,则下列关系正确的是( )A、T3=2
| ||||
B、T2=
| ||||
C、T2=
| ||||
D、T3=
|
分析:根据开普勒第三定律:
=k,k是与卫星无关的物理量,即所有卫星的比值k都相同,代入数据计算即可,其中圆轨道的a为圆的半径,椭圆轨道的a等于半长轴.
| a3 |
| T2 |
解答:解:AD、根据开普勒第三定律:
=k
所以
=
=
解得
=2
即T3=2
T1
故A正确、D错误.
B、根据开普勒第三定律:
=k
所以
=
=(
)3=(
)3
解得
=
即T2=
T1
故B错误.
C、根据开普勒第三定律:
=k
所以
=
=(
)3=(
)3
解得
=
即T2=
T3.
故C正确.
故选:AC.
| a3 |
| T2 |
所以
| T32 |
| T12 |
| R33 |
| R13 |
| 23 |
| 1 |
解得
| T3 |
| T1 |
| 2 |
即T3=2
| 2 |
故A正确、D错误.
B、根据开普勒第三定律:
| a3 |
| T2 |
所以
| T22 |
| T12 |
(
| ||
| R13 |
| ||
| R1 |
| 3 |
| 2 |
解得
| T2 |
| T1 |
3
| ||
| 4 |
即T2=
3
| ||
| 4 |
故B错误.
C、根据开普勒第三定律:
| a3 |
| T2 |
所以
| T22 |
| T32 |
(
| ||
| R33 |
| ||
| 2R1 |
| 3 |
| 4 |
解得
| T2 |
| T3 |
3
| ||
| 8 |
即T2=
3
| ||
| 8 |
故C正确.
故选:AC.
点评:本题主要考查开普勒第三定律,即
=k.要注意的是椭圆轨道的a为半长轴,即a=
.
| a3 |
| T2 |
| R1+R3 |
| 2 |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
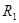 、周期为
、周期为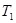 ;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为
;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为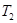 ;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为
;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为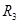 、周期为
、周期为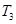 (轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点)。已知
(轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点)。已知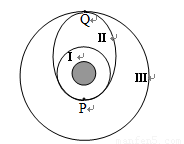
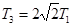 B.
B.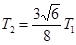
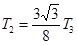 D.
D.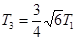

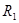 、周期为
、周期为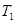 ;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为
;然后在P点点火加速,进入椭圆形转移轨道Ⅱ,在此轨道运行的卫星的周期为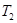 ;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为
;到达远地点Q时再次点火加速,进入远地圆轨道Ⅲ,在此轨道运行的卫星的轨道半径为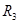 、周期为
、周期为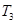 (轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点)。已知
(轨道Ⅱ的近地点为Ⅰ上的P点,远地点为轨道Ⅲ上的Q点)。已知