题目内容
17. 如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间和L3L4之间存在匀强磁场,磁感应强度B大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置由静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向,重力加速度g取10m/s2.则( )
如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间和L3L4之间存在匀强磁场,磁感应强度B大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置由静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向,重力加速度g取10m/s2.则( )| A. | 在0~t1时间内,通过线圈的电荷量为0.25C | |
| B. | 线圈匀速运动的速度大小为8m/s | |
| C. | 线圈的长度ad为1m | |
| D. | 0~t3时间内,线圈产生的热量为4.2J |
分析 t2~t3这段时间内线圈做匀速直线运动,线圈所受的安培力和重力平衡,根据平衡求出匀速直线运动的速度.通过线圈在t1~t2的时间间隔内,穿过线圈的磁通量没有改变,没有感应电流产生,线圈做匀加速直线运动,加速度为g,知ab边刚进磁场,cd边也刚进磁场,线圈的长度等于磁场宽度的2倍.根据运动学公式求出线圈的长度.根据感应电荷量的经验公式求解电荷量;根据能量守恒求出0~t3这段时间内线圈中所产生的电热.
解答 解:AC、t1~t2的时间间隔内线圈一直做匀加速直线运动,知ab边刚进上边的磁场时,cd边也刚进下边的磁场.设磁场的宽度为d,则线圈的长度:L′=2d
线圈下降的位移为:x=L′+d=3d,
则有:3d=vt-$\frac{1}{2}$gt2,
将v=8m/s,t=0.6s,
代入解得:d=1m;所以线圈的长度为L′=2d=2m.故C错误.
在0~t1时间内,cd边从L1运动到L2,通过线圈的电荷量为:q=$\overline{I}$t=$\frac{BL\overline{v}t}{R}$=$\frac{BLd}{R}$=0.25C.故A正确.
B、根据平衡有:mg=BIL,而I=$\frac{BLv}{R}$,联立两式解得:v=$\frac{mgR}{{B}^{2}{L}^{2}}$=8m/s.故B正确.
D、0~t3时间内,根据能量守恒得:Q=mg(3d+2d)-$\frac{1}{2}$mv2=0.1×10×(3+2)J-$\frac{1}{2}$×0.1×82J=1.8J.故D错误.
故选:AB.
点评 解决本题的关键理清线圈的运动情况,选择合适的规律进行求解,本题的难点就是通过线圈匀加速直线运动挖掘出下落的位移为磁场宽度的3倍.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
7. 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )| A. | 导体框中产生的感应电流方向相同 | B. | 导体框中产生的焦耳热相同 | ||
| C. | 导体框ab边两端电势差相同 | D. | 通过导体框截面的电荷量相同 |
8. 质量为m的滑块,沿着高为h、长为L的粗糙的固定斜面匀速下滑,在滑块从斜面顶端滑至底端的过程中,下列说法中不正确的是( )
质量为m的滑块,沿着高为h、长为L的粗糙的固定斜面匀速下滑,在滑块从斜面顶端滑至底端的过程中,下列说法中不正确的是( )
 质量为m的滑块,沿着高为h、长为L的粗糙的固定斜面匀速下滑,在滑块从斜面顶端滑至底端的过程中,下列说法中不正确的是( )
质量为m的滑块,沿着高为h、长为L的粗糙的固定斜面匀速下滑,在滑块从斜面顶端滑至底端的过程中,下列说法中不正确的是( )| A. | 重力对滑块所做的功为mgL | B. | 支持力对滑块做的功为0 | ||
| C. | 滑块克服摩擦力做的功为mgh | D. | 合外力对物体做的功为0 |
5. 如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两光滑斜面由静止自由滑下,在物体下滑到斜面底端的过程中,下列说法中正确的是( )
如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两光滑斜面由静止自由滑下,在物体下滑到斜面底端的过程中,下列说法中正确的是( )
 如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两光滑斜面由静止自由滑下,在物体下滑到斜面底端的过程中,下列说法中正确的是( )
如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两光滑斜面由静止自由滑下,在物体下滑到斜面底端的过程中,下列说法中正确的是( )| A. | 两物体所受重力的冲量相同 | |
| B. | 两物体所受合力的冲量相同 | |
| C. | 两物体到达斜面底端时的动量不同 | |
| D. | 两物体到达斜面底端时的动量水平分量相同 |
12.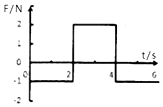 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )| A. | 0~6s内拉力做的功为零 | B. | 2~4s内拉力对物体做功为零 | ||
| C. | 6s末物体的动量为零 | D. | 2~4s内拉力对物体的冲量为零 |
11.在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步.在对以下几位物理学家在电磁学领域内所作科学贡献的叙述中,错误的说法是( )
| A. | 富兰克林不仅发现雷电现象的本质,还最早认识了尖端放电的重要性,并由此提出了避雷针的设想 | |
| B. | 法拉第提出电荷周围存在“场”,并创造性地用“电力线(即电场线)”形象地描述电场 | |
| C. | 英国物理学家焦耳通过一系列实验发现了焦耳定律Q=I2Rt | |
| D. | 奥斯特发现了电流的磁效应,并总结出了左手定则 |
 有一小灯泡上标有“4.8V 2W”的字样,某同学为了测量小灯泡在不同电压下的电功率,从实验室找到以下器材:
有一小灯泡上标有“4.8V 2W”的字样,某同学为了测量小灯泡在不同电压下的电功率,从实验室找到以下器材:

 如图,绝缘、光滑斜面倾角θ=37°,在区域I内有垂直于斜面向上的匀强磁场,区域II内有垂直于斜面向下的匀强磁场,磁感应强度大小均为B=1T,宽度均为d=0.4m,MN为两磁场的分界线.质量为0.06kg的矩形线框abcd,边长分别为L=0.6m和d=0.4m,置于斜面上端某处,ab边与磁场边界、斜面底边平行.由静止释放线框,线框沿斜面下滑,恰好匀速进入区域I.已知线框的总电阻R=0.5Ω.
如图,绝缘、光滑斜面倾角θ=37°,在区域I内有垂直于斜面向上的匀强磁场,区域II内有垂直于斜面向下的匀强磁场,磁感应强度大小均为B=1T,宽度均为d=0.4m,MN为两磁场的分界线.质量为0.06kg的矩形线框abcd,边长分别为L=0.6m和d=0.4m,置于斜面上端某处,ab边与磁场边界、斜面底边平行.由静止释放线框,线框沿斜面下滑,恰好匀速进入区域I.已知线框的总电阻R=0.5Ω.