题目内容
如图所示,匝数为100匝、面积为0.01m2的线圈,处于磁感应强度B1为 T的匀强磁场中.当线圈绕O1O2以转速n为300r/min匀速转动时,电压表、电流表的读数分别为7V、l A.电动机的内阻r为1Ω,牵引一根原来静止的、长L为1m、质量m为0.2kg的导体棒MN沿轨道上升.导体棒的电阻R为1Ω,架在倾角为30°的框架上,它们处于方向与框架平面垂直、磁感应强度B2为1T的匀强磁场中.当导体棒沿轨道上滑1.6m时获得稳定的速度,这一过程中导体棒上产生的热量为4J.不计框架电阻及一切摩擦,g取10m/s2.求:
T的匀强磁场中.当线圈绕O1O2以转速n为300r/min匀速转动时,电压表、电流表的读数分别为7V、l A.电动机的内阻r为1Ω,牵引一根原来静止的、长L为1m、质量m为0.2kg的导体棒MN沿轨道上升.导体棒的电阻R为1Ω,架在倾角为30°的框架上,它们处于方向与框架平面垂直、磁感应强度B2为1T的匀强磁场中.当导体棒沿轨道上滑1.6m时获得稳定的速度,这一过程中导体棒上产生的热量为4J.不计框架电阻及一切摩擦,g取10m/s2.求:(1)若从线圈处于中性面开始计时,写出电动势的瞬时表达式;
(2)导体棒MN的稳定速度;
(3)导体棒MN从静止至达到稳定速度所用的时间.

【答案】分析:(1)从线圈处于中性面开始计时,电动势的瞬时表达式e=Emsinωt.而Em=NB1Sω.
(2)导体棒MN的稳定速度时有F=mgsinθ+B2I′L,此时的电流 ,根据能量守恒求出电动机的输出功率
,根据能量守恒求出电动机的输出功率 ,则F=
,则F= ,联立求出稳定速度v.
,联立求出稳定速度v.
(3)根据能量守恒 求出导体棒MN从静止至达到稳定速度所用的时间.
求出导体棒MN从静止至达到稳定速度所用的时间.
解答:解:(1)线圈转动过程中电动势的最大值为
Em=NB1Sω=NB1S?2πn= .
.
则线圈从中性面开始计时的电动势瞬时表达式为e=Emsinωt=10sin10πtV
(2)棒达到稳定速度时,电动机的电流I=1A
电动机的输出功率
又P出=Fv
而棒产生的感应电流
稳定时棒处于平衡状态,故有:
F=mgsinθ+B2I′L
由以上各式代入数值,得棒的稳定速度v=2m/s.
(3)由能量守恒得
其中h=xsinθ=1.6sin30°=0.80m
所以t=1.0s.
点评:解决本题的关键掌握从线圈处于中性面开始计时,电动势的瞬时表达式e=Emsinωt以及峰值Em=NB1Sω.在该题中第(3)问较难,因为棒子上升的过程为变加速运动,然后以稳定速度运动.根据能量守恒,以及抓住发动机的输出功率不变进行求解.
(2)导体棒MN的稳定速度时有F=mgsinθ+B2I′L,此时的电流
 ,根据能量守恒求出电动机的输出功率
,根据能量守恒求出电动机的输出功率 ,则F=
,则F= ,联立求出稳定速度v.
,联立求出稳定速度v.(3)根据能量守恒
 求出导体棒MN从静止至达到稳定速度所用的时间.
求出导体棒MN从静止至达到稳定速度所用的时间.解答:解:(1)线圈转动过程中电动势的最大值为
Em=NB1Sω=NB1S?2πn=
 .
.则线圈从中性面开始计时的电动势瞬时表达式为e=Emsinωt=10sin10πtV
(2)棒达到稳定速度时,电动机的电流I=1A
电动机的输出功率

又P出=Fv
而棒产生的感应电流

稳定时棒处于平衡状态,故有:
F=mgsinθ+B2I′L
由以上各式代入数值,得棒的稳定速度v=2m/s.
(3)由能量守恒得

其中h=xsinθ=1.6sin30°=0.80m
所以t=1.0s.
点评:解决本题的关键掌握从线圈处于中性面开始计时,电动势的瞬时表达式e=Emsinωt以及峰值Em=NB1Sω.在该题中第(3)问较难,因为棒子上升的过程为变加速运动,然后以稳定速度运动.根据能量守恒,以及抓住发动机的输出功率不变进行求解.

练习册系列答案
相关题目
 如图所示,匝数为100、边长为0.2m的正方形线圈,在磁感应强度B为2T的匀强磁场中,从中性面开始以10πrad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,π2=10,则开始转动0.05s内R上的热量为多少焦耳?
如图所示,匝数为100、边长为0.2m的正方形线圈,在磁感应强度B为2T的匀强磁场中,从中性面开始以10πrad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,π2=10,则开始转动0.05s内R上的热量为多少焦耳?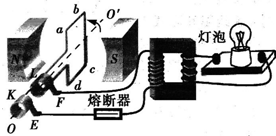 如图所示,匝数为100匝的矩形线圈abcd处于磁感应强度B=
如图所示,匝数为100匝的矩形线圈abcd处于磁感应强度B=
 T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10π rad/s匀速转动。线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是
T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10π rad/s匀速转动。线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是 s内在电阻R上产生的热量为多少焦耳?
s内在电阻R上产生的热量为多少焦耳? 