题目内容
如图所示，水平台面光滑，穿过两光滑轻质定滑轮的轻绳两端分别连接着物体A和B，A、B的质量分别为M和m，滑轮到台面高为h，用手按住A此时A端绳与台面的夹角 a=30°，然后放手，使它们运动，已知A始终没有离开台面，则A的最大速度为（ ）
A．
B．
C．2
D．
【答案】分析：对M和m组成的系统，机械能守恒，当α=90°时，A的速度最大，根据系统机械能守恒求出A的最大速度．
解答：解：当A的速度最大时，α=90°，此时物体沿绳子方向上的分速度为零，则B的速度为零．
根据系统机械能守恒定律得，mg（
）=
．
解得v=
．故B正确，A、C、D错误．
故选B．
点评：解决本题的关键知道A、B系统机械能守恒，以及知道当A的速度最大时，B的速度为零．
解答：解：当A的速度最大时，α=90°，此时物体沿绳子方向上的分速度为零，则B的速度为零．
根据系统机械能守恒定律得，mg（
）=．解得v=
．故B正确，A、C、D错误．故选B．
点评：解决本题的关键知道A、B系统机械能守恒，以及知道当A的速度最大时，B的速度为零．
练习册系列答案
相关题目
如图所示，水平台面AB距地面的高度h=0.80m．有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动，滑块与平台间的动摩擦因数μ=0.25．滑块运动到平台边缘的B点后水平飞出．已知AB=2.2m．不计空气阻力，g取10m/s2，结果保留2位有效数字．求：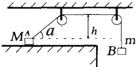
如图所示，水平台面光滑，穿过两光滑轻质定滑轮的轻绳两端分别连接着物体A和B，A、B的质量分别为M和m，滑轮到台面高为h，用手按住A此时A端绳与台面的夹角 a=30°，然后放手，使它们运动，已知A始终没有离开台面，则A的最大速度为（ ）