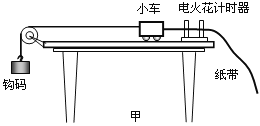
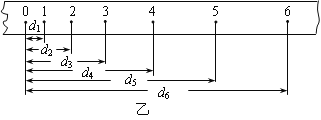
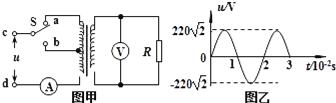
��Ŀ����
����Ŀ��һ̽�ն�Ա��̽��ʱ����һɽ����ɽ����һ����ֱ����һ����������������״���˶�Ա��ɽ������ֱһ�������ٶ�v0��ˮƽ����������һ�����森��ͼ��ʾ���Թ���O��Ϊԭ�㽨������ϵxOy.��֪��ɽ����ֱһ��ĸ߶�Ϊ2h������������߷���Ϊy��![]() x2��̽�ն�Ա������Ϊm.����Ϊ�ʵ������Կ����������������ٶ�Ϊg.
x2��̽�ն�Ա������Ϊm.����Ϊ�ʵ������Կ����������������ٶ�Ϊg.

(1)������䵽����ʱ�Ķ��ܣ�
(2)����ˮƽ�������ٶ�Ϊ���ʱ������������ʱ�Ķ�����С�����ܵ���СֵΪ���٣�
���𰸡�(1)![]() (2)
(2) ![]() mgh.
mgh.
�������������������1����ö�Ա�ڿ����˶���ʱ��Ϊt �������������ĺ�����Ϊx ��������Ϊy �����˶�ѧ��ʽ����֪������
x=v0t![]()
�����⣺![]()
�ɻ�е���غ��֪�䵽����ʱ�Ķ���Ϊ��![]()
������ã�![]()
��2����![]() �ɸ�дΪ
�ɸ�дΪ![]()
��![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]()

��ϰ��ϵ�д�
�����Ŀ