题目内容
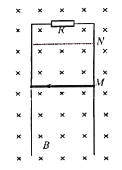
【题目】如图所示，在磁感应强度为
的水平匀强磁场中，有一竖直放置的光滑的平行金属导轨，导轨平面与磁场垂直，导轨间距为
，顶端接有阻值为
的电阻。将一根金属棒从导轨上的
处以速度
竖直向上抛出，棒到达
处后返回，回到出发点时棒的速度为抛出时的一半。已知棒的长度为，质量为
，电阻为
。金属棒始终在磁场中运动，处于水平且与导轨接触良好，忽路导轨的电阻。重力加速度为
。
（1）金属棒从点被抛出至落回点的整个过程中，求：
a．电阻消耗的电能；
b．金属棒运动的时间。
（2）经典物理学认为，金属的电阻源于定向运动的自由电子与金属离子的碰撞。已知元电荷为
。求当金属棒向下运动达到稳定状态时，棒中金属离子对一个自由电子沿棒方向的平均作用力大小。
【答案】(1)a.
b.
(2)
【解析】
（1）a．金属棒从M点被抛出至落回M点的整个过程中，由能量守恒
回路中消耗的电能
电阻R消耗的电能
b．金属棒从M点被抛出至落回M点的整个过程中，取向下为正方向，由动量定理得：
将整个运动过程划分成很多小段，可认为在每个小段中感应电动势几乎不变，设每小段的时间为△t．则安培力的冲量
I安=Bi1L△t+Bi2L△t+Bi3L△t+…
I安=BL（i1△t+i2△t+i3△t+…）
I安=BLq
又
，
，
因为△Φ=0，所以
I安=0
解得
(2)当金属棒向下运动达到稳定状态时
mg=Fm
其中
解得
沿棒方向，棒中自由电子受到洛伦兹力evmB、电场力eE和金属离子对它的平均作用力f作用．因为棒中电流恒定，所以自由电子沿棒的运动可视为匀速运动．
则
f+eE=evmB
又
解得
练习册系列答案
名校课堂系列答案
相关题目
