题目内容
如图所示，一质量为m的小球，以初速度v沿水平方向射出，恰好垂直地射到一倾角为30°的固定斜面上，并立即反方向弹回．已知反弹速度的大小是入射速度大小的
，则下列说法正确的是（ ）
A．在碰撞中斜面对小球的冲量大小为
mvB．在碰撞中斜面对小球的冲量大小为
mvC．小球在竖直方向下落的距离与在水平方向通过的距离之比为
D．小球在竖直方向下落的距离与在水平方向通过的距离之比为
【答案】分析：小球垂直斜面入射可知小球的速度方向，由平抛运动规律可求得小球飞行时间及速度；由动量定理可求得斜面对小球的冲量；由位移公式可求得竖直和水平距离之比．
解答：解：小球的速度与竖直方向成30°角，则此时的合速度v=
=2v，反弹后的速度v'=
×2v=
v，由动量定理可知，冲量I=-
mv-2mv=-
mv；故A正确；B错误；
小球的竖直速度vy=2v×cos30°=
v，由vy=gt求得t=
，水平位移x=vt=
，竖直位移y=
gt2=
，故竖直方向上落的距离与水平方向的距离之比为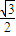
，故C错误，D正确；
故选AD．
点评：（1）解决平抛运动应注意应用运动的合成与分解，知道末速度的方向即可求出需要的合速度及竖直速度等，则位移可解；
（2）动量定理的应用中一定要注意其矢量性，明确相应的方向．
解答：解：小球的速度与竖直方向成30°角，则此时的合速度v=
=2v，反弹后的速度v'=×2v=v，由动量定理可知，冲量I=-mv-2mv=-mv；故A正确；B错误；小球的竖直速度vy=2v×cos30°=
v，由vy=gt求得t=，水平位移x=vt=，竖直位移y=gt2=，故竖直方向上落的距离与水平方向的距离之比为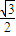，故C错误，D正确；故选AD．
点评：（1）解决平抛运动应注意应用运动的合成与分解，知道末速度的方向即可求出需要的合速度及竖直速度等，则位移可解；
（2）动量定理的应用中一定要注意其矢量性，明确相应的方向．
练习册系列答案
相关题目
如图所示，一质量为m，带电荷量为+q的小物体，在水平方向的匀强磁场B中，从倾角为
如图所示，一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈，从h1=5m的高处由静止开始下落，然后进入高度为h2（h2＞L）的匀强磁场．下边刚进入磁场时，线圈正好作匀速运动．线圈的下边通过磁场所经历的时间t=0.15s．取g=10m/s2
如图所示，一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑．现对物块施加一个竖直向下的恒力F．则物块（ ）
如图所示，一质量为m的小球，用长为l的轻绳悬挂于O点，小球在水平恒力F的作用下，从最低点A点拉至B点的过程中，力F所做的功为（ ）
如图所示，一质量为m=1.0×10-2kg，带电量为q=1.0×10-6C的小球，用绝缘细线悬挂在水平向右的匀强电场中，假设电场足够大，静止时悬线向左与竖直方向成37°角．小球在运动过程电量保持不变，重力加速度g取10m/s2．