题目内容
 竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中,B=1.1T,管道半径R=0.8m,其直径POQ在竖直线上,在管口P处以2m/s的速度水平射入一个带电小球,可把它视为质点,其电荷量为lO-3C(g=lOm/s2),试求:
竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中,B=1.1T,管道半径R=0.8m,其直径POQ在竖直线上,在管口P处以2m/s的速度水平射入一个带电小球,可把它视为质点,其电荷量为lO-3C(g=lOm/s2),试求:(1)小球滑到Q处的速度为多大?
(2)若小球从Q处滑出瞬间,管道对它的弹力正好为零,小球的质量为多少?
分析:(1)小球从管口P滑到Q的过程中,洛伦兹力和轨道的弹力不做功,只有重力做功,根据机械能守恒定律求小球滑到Q处的速度;
(2)若小球从Q处滑出瞬间,管道对它的弹力正好为零,由洛伦兹力和重力的合力提供向心力,根据牛顿第二定律列式求小球的质量.
(2)若小球从Q处滑出瞬间,管道对它的弹力正好为零,由洛伦兹力和重力的合力提供向心力,根据牛顿第二定律列式求小球的质量.
解答:解:(1)从P→Q,洛伦兹力和轨道的弹力不做功,只有重力做功,小球的机械能守恒定律,则得:
m
+2mgR=
m
代入数据解得:vQ=
=
m/s=6m/s
(2)小球从Q处滑出瞬间,管道对它的弹力正好为零,则由洛伦兹力和重力的合力提供向心力,根据牛顿第二定律得:
qvQB-mg=m
代入解得,m=
=
kg=1.2×10-4kg
答:
(1)小球滑到Q处的速度为6m/s.
(2)若小球从Q处滑出瞬间,管道对它的弹力正好为零,小球的质量为1.2×10-4kg.
| 1 |
| 2 |
| v | 2 P |
| 1 |
| 2 |
| v | 2 Q |
代入数据解得:vQ=
|
| 22+4×10×0.8 |
(2)小球从Q处滑出瞬间,管道对它的弹力正好为零,则由洛伦兹力和重力的合力提供向心力,根据牛顿第二定律得:
qvQB-mg=m
| ||
| R |
代入解得,m=
| qvQB | ||||
g+
|
| 10-3×6×1.1 | ||
10+
|
答:
(1)小球滑到Q处的速度为6m/s.
(2)若小球从Q处滑出瞬间,管道对它的弹力正好为零,小球的质量为1.2×10-4kg.
点评:本题在带电体在复合场中运动的类型,抓住洛伦兹力不做功,根据机械能守恒和牛顿第二定律求解.

练习册系列答案
相关题目

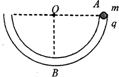 如图所示,在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷,将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无作用力.若小球所带电荷量很小,不影响O点处的点电荷的电场,则放于圆心O处的点电荷在OB连线的中点处的电场强度大小( )
如图所示,在竖直放置的半圆形光滑绝缘细管的圆心O处放一点电荷,将质量为m、电荷量为q的小球从管的水平直径的端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无作用力.若小球所带电荷量很小,不影响O点处的点电荷的电场,则放于圆心O处的点电荷在OB连线的中点处的电场强度大小( )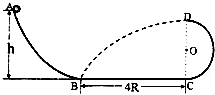 如图所示,AB为弧形光滑轨道,CD是一半径为R的竖直放置的半圆形光滑轨道,D点在C点正上方,BC为一段粗糙的水平轨道,动摩擦因数为μ=0.25,BC=4R,现在A点从静止释放一个质量为m的小球,小球沿轨道滑行,最后从D点飞出,恰好落在了B点,试求:
如图所示,AB为弧形光滑轨道,CD是一半径为R的竖直放置的半圆形光滑轨道,D点在C点正上方,BC为一段粗糙的水平轨道,动摩擦因数为μ=0.25,BC=4R,现在A点从静止释放一个质量为m的小球,小球沿轨道滑行,最后从D点飞出,恰好落在了B点,试求: 竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中,B=1.1T,管道半径R=0.8m,其直径POQ在竖直线上,在管口P处以2m/s的速度水平射入一个带电小球(可视为质点),其电荷量为10-4C(g取10m/s2),小球滑到Q处时的速度大小为
竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中,B=1.1T,管道半径R=0.8m,其直径POQ在竖直线上,在管口P处以2m/s的速度水平射入一个带电小球(可视为质点),其电荷量为10-4C(g取10m/s2),小球滑到Q处时的速度大小为