题目内容
（10分）如图所示，一轻绳通过无摩擦的定滑轮与放在倾角为30°的光滑斜上的物体m1连接，另一端和套在光滑竖直杆上的物体m2连接，图中定滑轮到竖直杆的距离为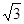
m，又知当物体m2由图中位置（连接m2的轻绳此时水平）从静止开始下滑1m时，m1和m2受力恰好平衡。试求：（g取10 m/s2 ）
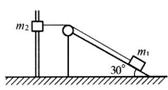
（1）m2下滑过程中的最大速度。
（2）m2下滑的最大距离。
【答案】
（1）2．15m/s （2）
=2．31m
【解析】本题考查连接体问题中的动能定理或机械能守恒定律的应用，m2下滑过程中受到绳子的拉力、杆的弹力、和重力作用，m1受到绳子的拉力、支持力、重力作用，由绳子对m2和m1的拉力大小相等，绳子的拉力与两物体重力的关系可求得两物体的质量之比，以系统作为一个整体为研究对象，整个系统没有摩擦力作用，机械能守恒，列出公式，以m2为研究对象把速度进行分解，沿着绳子方向的分速度为m1上升时的速度
① m2下滑1米时，由几何关系可知θ＝300
② 对m2、m1进行受力分析，由平衡条件可知
③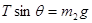 
④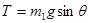 
⑤ 解得：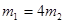
⑥ 以m1、m2构成得系统为研究对象，由于只有重力
⑦ 做功，所以机械能守恒
⑧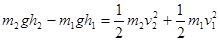 
⑨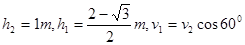 
⑩ 联立解得：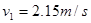
⑪ ②令m2下滑得最大距离为H，由系统机械能守恒可得
⑫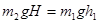 
⑬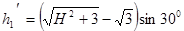 
⑭ 解得：H=2.3m
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．则（ ）
（2006?洪泽县模拟）如图所示，一轻绳通过一光滑定滑轮，两端各系一质量分别为m1和m2的物体，m1放在地面上，当m2的质量发生变化时，m1的加速度a的大小与m2的关系大体如图中的（ ）
（2013?娄底一模）如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，系统从图示位置由静止释放后，A先沿杆向上运动，并能到达与O点等高的C点的上方．设上升过程中某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．不计空气阻力，则（ ）
如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为vA，小球B运动的速度大小为vB，轻绳与杆的夹角为θ．则（ ）
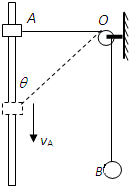如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，小球B与物块A质量相等，杆两端固定且足够长．现将物块A由静止从与O等高位置释放后，下落到轻绳与杆的夹角为θ时物块A运动的速度大小为vA，小球B运动的速度大小为vB．则下列说法中正确的是（ ）| A、vA=vB | B、vB=vAsinθ | C、小球B增加的重力势能等于物块A减少重力势能 | D、小球B增加的机械能等于物块A减少机械能 |