Question

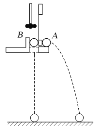
【题目】如图，光滑水平面AB与竖直面内的粗糙半圆形导轨在B点相接，导轨半径为R。一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，它经过B点的速度为v1，之后沿半圆形导轨运动，刚好能沿导轨到达C点。重力加速度为g，忽略空气阻力。求：

（1）弹簧压缩至 A 点时的弹性势能；

（2）物体沿半圆形导轨运动过程中所受摩擦阻力做的功；

（3）物体的落点与B点的距离。

Answer 1

【答案】（1）；（2）；（3）

【解析】

(1)由能量守恒可知，弹簧的弹性势能转化为物体的动能，所以弹簧压缩至A点时的弹性势能

(2)对物体，B→C，由动能定理有

刚好能沿导轨到达C点时，有重力提供向心力

联立解得

(3) 刚好能沿导轨到达C点时，有重力提供向心力

C点时抛出后竖直方向有

水平方向位移为

联立解得落点与B点的距离为。