Question

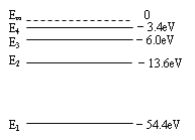
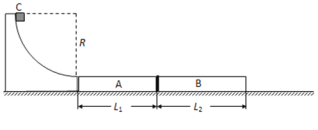
【题目】如图，质量均为2m的木板A、B并排静止在光滑水平地面上，A左端紧贴固定于水平面的半径为R的四分之一圆弧底端，A与B、A与圆弧底端均不粘连。质量为m的小滑块C从圆弧顶端由静止滑下，经过圆弧底端后，沿A的上表面从左端水平滑上A，并在恰好滑到B的右端时与B一起匀速运动。已知重力加速度为g，C过圆弧底端时对轨道的压力大小为1.5mg，C在A、B上滑行时受到的摩擦阻力相同，C与B一起匀速运动的速度是C刚滑上A时的0.3倍，木板A的长度为L0。求：

(1)C从圆弧顶端滑到底端的过程中克服摩擦力做的功；

(2)木板B的长度L；

(3)C刚滑到B的右端时，A右端到B左端的水平距离s与木板B的长度L之比。

Answer 1

【答案】（1）；（2）；（3）

【解析】

(1)设到达圆弧底端时的速度为，轨道对支持力大小为，下滑过程克服摩擦力做的功为，由动能定理，有：

过底端时，由牛顿第二定律，有：

由牛顿第三定律，有：

联立解得：

(2)设刚滑过到达时，的速度为，、的速度为，、共同速度为，与、B间的摩擦力为，从滑上到刚滑到这个过程，和、组成的系统动量守恒，由动量守恒守律：

由功能关系：

滑上到与共速这个过程，对和组成的系统，由动量守恒定律：

由功能关系：

代入可得：

，

联立可得：

(2)设从滑上到与共速所经历的时间为，对由动量定理则有：

设在时间内通过的距离为，对应用动能定理：

联立并代入，得：