题目内容
如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角为2θ，若要小球离开锥面，则小球的角速度至少为多少？（重力加速度为g）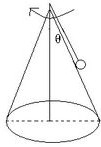
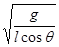
解析试题分析：当小球对斜面没有压力时拉力F和小球重力提供小球做圆周运动的向心力，小球即将离开斜面，
即设绳对球的拉力为F，小球做圆周运动的半径为R
由几何关系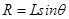
3分
拉力F和小球重力提供小球做圆周运动的向心力：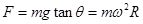
3分
联立解得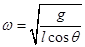
3分
考点：考查了圆周运动实例分析
点评：本题的关键是找出小球离开锥面的临界条件
练习册系列答案
相关题目
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内作半径不同的匀速圆周运动，其中球P的轨道半径较大，则可判定（ ）
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则（ ） 如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则 
| A．球P的角速度较小 | B．球P的向心力较小 |
| C．球P的加速度较大 | D．球P的线速度较大 |
