题目内容
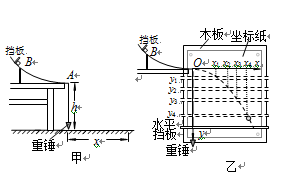
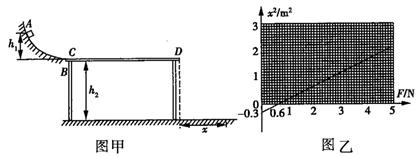
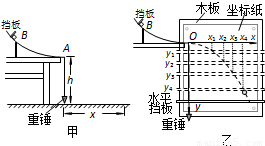
如图甲所示,水平桌面上固定有一位于竖直平面内的弧形轨道A,其下端的切线是水平的,轨道的厚度可忽略不计.将小铁块B从轨道的固定挡板处由静止释放,小铁块沿轨道下滑,最终落到水平地面上.若测得轨道末端距离水平地面的高度为h,小铁块从轨道飞出到落地的水平位移为x,已知当地的重力加速度为g.(1)小铁块从轨道末端飞出时的速度v=______
【答案】分析:(1)将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动,由高度h求出时间,由v=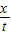 求出小铁块从轨道末端飞出时的速度.
求出小铁块从轨道末端飞出时的速度.
(2)根据功能关系:小铁块下滑过程中克服摩擦力所做功等于小铁块机械能的减小量,来分析还需要测量的物理量.
(3)根据x=vt、y=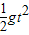 推出轨迹方程,分析斜率k,得出速度的表达式.
推出轨迹方程,分析斜率k,得出速度的表达式.
解答:解:(1)在竖直方向
由h=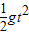 得,t=
得,t=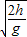
在水平方向
v=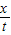 =x
=x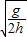
(2)还需要测量的物理量有小铁块沿轨道下滑的高度H和小铁块的质量m.
因为根据功能关系得
小铁块下滑过程中克服摩擦力所做功W=mgH-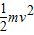 =mgH-
=mgH-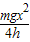 .
.
(3)由x=vt、y=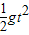 得到
得到
轨迹方程为y=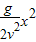
则y-x2的图线是过原点的直线,其斜率k=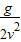
故v=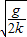
故本题答案是:
(1)x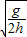
(2)小铁块沿轨道下滑的高度H和小铁块的质量m;mgH-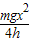
(3)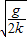
点评:本题考查迁移能力.平抛运动采用运动的合成与分解处理,通常分解为水平方向和竖直方向.第(3)问运用数学上参数方程分析轨迹方程,研究斜率的意义.
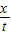 求出小铁块从轨道末端飞出时的速度.
求出小铁块从轨道末端飞出时的速度.(2)根据功能关系:小铁块下滑过程中克服摩擦力所做功等于小铁块机械能的减小量,来分析还需要测量的物理量.
(3)根据x=vt、y=
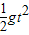 推出轨迹方程,分析斜率k,得出速度的表达式.
推出轨迹方程,分析斜率k,得出速度的表达式.解答:解:(1)在竖直方向
由h=
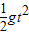 得,t=
得,t=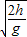
在水平方向
v=
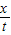 =x
=x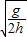
(2)还需要测量的物理量有小铁块沿轨道下滑的高度H和小铁块的质量m.
因为根据功能关系得
小铁块下滑过程中克服摩擦力所做功W=mgH-
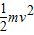 =mgH-
=mgH-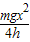 .
.(3)由x=vt、y=
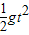 得到
得到轨迹方程为y=
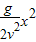
则y-x2的图线是过原点的直线,其斜率k=
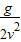
故v=
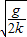
故本题答案是:
(1)x
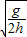
(2)小铁块沿轨道下滑的高度H和小铁块的质量m;mgH-
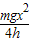
(3)
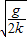
点评:本题考查迁移能力.平抛运动采用运动的合成与分解处理,通常分解为水平方向和竖直方向.第(3)问运用数学上参数方程分析轨迹方程,研究斜率的意义.

练习册系列答案
相关题目
 如图甲所示,水平桌面上固定有一位于竖直平面内的弧形轨道A,其下端的切线是水平的,轨道的厚度可忽略不计.将小铁块B从轨道的固定挡板处由静止释放,小铁块沿轨道下滑,最终落到水平地面上.若测得轨道末端距离水平地面的高度为h,小铁块从轨道飞出到落地的水平位移为x,已知当地的重力加速度为g.
如图甲所示,水平桌面上固定有一位于竖直平面内的弧形轨道A,其下端的切线是水平的,轨道的厚度可忽略不计.将小铁块B从轨道的固定挡板处由静止释放,小铁块沿轨道下滑,最终落到水平地面上.若测得轨道末端距离水平地面的高度为h,小铁块从轨道飞出到落地的水平位移为x,已知当地的重力加速度为g.