Question

【题目】如图甲所示，质量为m的相同木块A和木板B叠放在水平面上，A光滑且位于B的最右端，B与地面间动摩擦因数为，水平力作用在B上，A、B以的共同速度沿水平面向右匀速运动，后F加倍，前二者速度v随时间t的变化关系如图所示，．

试求的值；

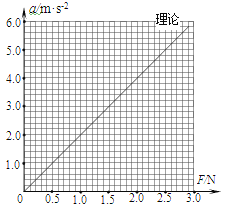
若B足够长，请在乙图中作出、B运动的图线，并标出时的纵坐标值；

若前不会从B上滑落，木板B至少有多长。

Answer 1

【答案】

【解析】

（1）由前二者速度v随时间t的变化关系可得，AB系统水平方向受力平衡，由平衡条件可得的值；

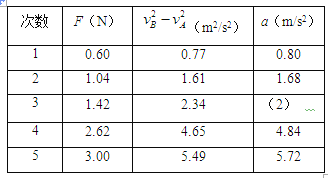
（2）根据共点力平衡求出滑动摩擦力的大小，结合滑动摩擦力公式求出动摩擦因数的大小；

（3），A运动状态不变，继续做匀速直线运动，B做匀加速运动，根据牛顿第二定律求出加速度，结合速度时间公式求出B的速度，作出图线；

（1）在内A、B做匀速直线运动，分析B根据平衡条件有：
而且：，解得：；

（2）在，A运动状态不变，继续做匀速直线运动，B做匀加速运动，根据牛顿第二定律得：，解得：
则在时B的速度为：
如图所示：

（3）根据（2）问所作图象知木板B长至少为。