题目内容
如图所示,表示一个平面上晶体物质微粒的排列情况,图上画出了三条等长线AB、AC和AD,在这三条线上物质微粒的数目均 (填“相同”或“不同”),因此我们可以得出的结论是 .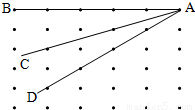
解答:解:晶体和非晶体的重要区别是:晶体有一定的熔点,非晶体没有一定的熔点.同时晶体中单晶体具有各向异性,而非晶体都各向同性.因此这三条线上物质微粒的数目均不同,从而得出结论为:晶体的物理性质是各向异性的或晶体在不同方向上的物理性质是不同的.
故答案为:不同;晶体的物理性质是各向异性的或晶体在不同方向上的物理性质是不同的.
点评:掌握固体的分类.掌握晶体和非晶体都异同点.本题考查的是晶体和非晶体的区别,难度不大,注意晶体与非晶体最本质的区别是组成物质的粒子在微观空间是否有序排列.

(18分)(1)如图所示,在“研究平抛物体运动”的实验中,有一张印有小方格的纸记录轨迹,小方格的边长L=2.5 cm。若小球在平抛运动过程中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=__________(用L、g表示),其值为__________ m/s;小球在b点的速度大小为__________ m/s。(取g=10 m/s2,计算结果全部取2位有效数字),
(2)一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系。
①首先,他们让一砝码做半径r为0.08m的圆周运动,数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω,如下表。请你根据表中的数据在图甲上绘出F-ω的关系图像。
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F/N | 2.42 | 1.90 | 1.43 | 0.97 | 0.76 | 0.50 | 0.23 | 0.06 |
| ω/rad·s-1 | 28.8 | 25.7 | 22.0 | 18.0 | 15.9 | 13.0 | 8.5 | 4.3 |
②通过对图像的观察,兴趣小组的同学猜测F与ω2成正比。你认为,可以通过进一步转换,做出____________关系图像来确定他们的猜测是否正确。
③在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图像,他们将三次实验得到的图像放在一个坐标系中,如图乙所示。通过对三条图像的比较、分析、讨论,他们得出F∝ r的结论,你认为他们的依据是___________________________________________________________。
④通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为__________。(计算结果取2位有效数字)
(1)在“研究平抛物体的运动”的实验中,为了描出物体的运动轨迹,实验应有下列各个步骤:
| A.以O为原点,画出与y轴相垂直的水平轴x轴; |
| B.把事先做的有缺口的纸片用手按在竖直木板上,使由斜槽上滚下抛出的小球正好从纸片的缺口中通过,用铅笔在白纸上描下小球穿过这个缺口的位置; |
| C.每次都使小球由斜槽上固定的标卡位置开始滚下,用同样的方法描出小球经过的一系列位置,并用平滑的曲线把它们连接起来,这样就描出了小球做平抛运动的轨迹; |
| D.用图钉把白纸钉在竖直木板上,并在木板的左上角固定好斜槽; |

在上述实验中,缺少的步骤F是___________________________________________,
正确的实验步骤顺序是__________________。
(2)如图所示,在“研究平抛物体运动”的实验中,用一张印有小方格的纸记录轨迹,小方格的边长l=1.25cm。若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为vo= (用l、g表示),其值是 (取g=9.8m/s2),小球在b点的速率是 。
(18分)(1)如图所示,在“研究平抛物体运动”的实验中,有一张印有小方格的纸记录轨迹,小方格的边长L=2.5 cm。若小球在平抛运动过程中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=__________(用L、g表示),其值为__________ m/s;小球在b点的速度大小为__________ m/s。(取g=10 m/s2,计算结果全部取2位有效数字),

(2)一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系。
①首先,他们让一砝码做半径r为0.08m的圆周运动,数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω,如下表。请你根据表中的数据在图甲上绘出F-ω的关系图像。
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
F/N |
2.42 |
1.90 |
1.43 |
0.97 |
0.76 |
0.50 |
0.23 |
0.06 |
|
ω/rad·s-1 |
28.8 |
25.7 |
22.0 |
18.0 |
15.9 |
13.0 |
8.5 |
4.3 |


②通过对图像的观察,兴趣小组的同学猜测F与ω2成正比。你认为,可以通过进一步转换,做出____________关系图像来确定他们的猜测是否正确。
③在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图像,他们将三次实验得到的图像放在一个坐标系中,如图乙所示。通过对三条图像的比较、分析、讨论,他们得出F∝ r的结论,你认为他们的依据是___________________________________________________________。
④通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为__________。(计算结果取2位有效数字)
(1)如图所示,在“研究平抛物体运动”的实验中,有一张印有小方格的纸记录轨迹,小方格的边长L=2.5 cm。若小球在平抛运动过程中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为v0=__________(用L、g表示),其值为__________ m/s;小球在b点的速度大小为__________ m/s。(取g=10 m/s2,计算结果全部取2位有效数字),

(2)一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系。
①首先,他们让一砝码做半径r为0.08m的圆周运动,数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω,如下表。请你根据表中的数据在图甲上绘出F-ω的关系图像。
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F/N | 2.42 | 1.90 | 1.43 | 0.97 | 0.76 | 0.50 | 0.23 | 0.06 |
| ω/rad·s-1 | 28.8 | 25.7 | 22.0 | 18.0 | 15.9 | 13.0 | 8.5 | 4.3 |


②通过对图像的观察,兴趣小组的同学猜测F与ω2成正比。你认为,可以通过进一步转换,做出____________关系图像来确定他们的猜测是否正确。
③在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图像,他们将三次实验得到的图像放在一个坐标系中,如图乙所示。通过对三条图像的比较、分析、讨论,他们得出F∝ r的结论,你认为他们的依据是___________________________________________________________。
④通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为__________。(计算结果取2位有效数字)
